Bonsoir et merci davoir répondu.
Non malheureusement on doit se débrouiller tout seul
Je me suis renseigné sur la méthode de Gauss et jy arrive sur des exemples simples :
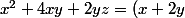^2-(2y-(z/2))^2+ (z/2)^2)
cependant jai un doute quant à mon exercice .
Voilà ce que je trouve pour la première étape:
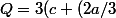)^2-3(2a/3)^2-3b^2+2ab+2ad-4bd-2cd)
Ce qui me semble étrange car j'ai un "3" et un "-3" en dehors des "carrés", cela est il possible ?
Au final, en continuant de cette façon je trouve
)^2-3(b-(a/3))^2+(a+d)^2+(c-d)^2+2(b-d)^2-2a^2-2b^2-c^2-4d^2)
En développant, je retombe sur la forme de l'énoncé.
Il me semble avoir compris que la signature correspond à la paire formée des termes positifs/négatifs et le rang correspondrait au nombre de termes, j'aurai donc rang(4,5) et signature 9 ?
Je vous remercie encore de me consacrer une partie de votre temps.
