Matrice de passage
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 22 Avr 2012, 11:11
par loytef » 22 Avr 2012, 11:11
Bonjour, Je n'arrive pas à résoudre une question.
J'ai
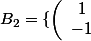,\left(\begin{array}{c} 1\\ 2 \end{array}\right)\})
qui est une base de
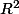
.
On considère l'application f définie de R^3 dans R^2 par :f
\right)=\left(\begin{array}{c} x+z\\ x-y \end{array}\right))
.
Calculer
)
où

est la base canonique de R^3.
Faut-il calculer la matrice de passage P de

à

?
Sinon comment faire ?
merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Avr 2012, 16:42
par Joker62 » 22 Avr 2012, 16:42
Bonjour.
Calcules l'image de chaque vecteur de la base canonique de R^3 et exprime ces images en fonctions des vecteurs de B_2
Tu auras la matrice de f.
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 22 Avr 2012, 21:36
par loytef » 22 Avr 2012, 21:36
Joker62 a écrit:Bonjour.
Calcules l'image de chaque vecteur de la base canonique de R^3 et exprime ces images en fonctions des vecteurs de B_2
Tu auras la matrice de f.
Les vecteurs de la base canonique de R^3 sont :
e1= (1,0,0), e2=(0,1,0), e3=(0,0,1)
f(e1)=(1,1)
f(e2)=(0,-1)
f(e3)=(1,0)
Et après je vois pas comment faire pour exprimer ces images en fonction de B_2.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 23 Avr 2012, 00:00
par Joker62 » 23 Avr 2012, 00:00
Ensuite il faut exprimer ces images en fonction des vecteurs de la base B_2
Par exemple
On cherche a et b tels que
(1;1) = a*(1;-1) + b*(1;2)
D'où 1 = a + b et 1 = 2b - a
Ainsi b = 2/3 et a = 1/3
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 23 Avr 2012, 09:04
par loytef » 23 Avr 2012, 09:04
Joker62 a écrit:Ensuite il faut exprimer ces images en fonction des vecteurs de la base B_2
Par exemple
On cherche a et b tels que
(1;1) = a*(1;-1) + b*(1;2)
D'où 1 = a + b et 1 = 2b - a
Ainsi b = 2/3 et a = 1/3
Ok. La matrice f est
)
Juste par curiosité n'y a-il pas une autre méthode avec la formule P^-1AP ?
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 24 Avr 2012, 16:49
par loytef » 24 Avr 2012, 16:49
ma matrice f est-elle correct ?
merci
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 24 Avr 2012, 18:19
par loytef » 24 Avr 2012, 18:19
loytef a écrit:ma matrice f est-elle correct ?
merci
J'ai une dernière question que je n'arrive pas à résoudre:
Soit l'application linéaire g de R^2 dans R^3 définie par
)
(
avec  base canonique de R^3
base canonique de R^3) =
)
Déterminer la matrice de g dans les bases canoniques de R^2 et R^3.
Je suis arrivé à: g(1,-1)=e2
g(1,2) = 3e1 +e2 + 3e3 mais après je ne sais plus comment faire :triste:
help
merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2012, 18:29
par Joker62 » 24 Avr 2012, 18:29
Bonsoir,
Pareil que pour le cas précédent.
Il faut calculer g(e_1) avec e_1 = (1;0)
et g(e_2) avec e_2 = (0;1)
et exprimer les images les vecteurs de B^3.
Sinon, on peut bien sûr utiliser la formule avec la matrice de passage mais il faut faire ça dans le bon ordre. Ce qui n'est pas toujours facile :)
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 24 Avr 2012, 18:32
par loytef » 24 Avr 2012, 18:32
Joker62 a écrit:Bonsoir,
Pareil que pour le cas précédent.
Il faut calculer g(e_1) avec e_1 = (1;0)
et g(e_2) avec e_2 = (0;1)
et exprimer les images les vecteurs de B^3.
Sinon, on peut bien sûr utiliser la formule avec la matrice de passage mais il faut faire ça dans le bon ordre. Ce qui n'est pas toujours facile

Ok mais comment calculer g(e_1) vu que je n'ai pas directement g?
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 24 Avr 2012, 19:07
par loytef » 24 Avr 2012, 19:07
Ok après avoir fait (1;0) = 2/3*(1;-1) + 1/3*(1;2) comment faire pour exprimer ces vecteurs dans B_3
Pour la matrice de passage, il faut une matrice de passage de B_3 à B_2 ou B_2 à B_3 ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2012, 19:12
par Joker62 » 24 Avr 2012, 19:12
Alors tu as M la matrice de f dans les bases B_2 ; B_3
On veut la matrice M' de f dans les bases B'_2; B_3
ou B'_2 est la base canonique de R^2
Il faut donc la matrice de passage de B_2 vers B'_2. On a la note P.
On a alors
M' = M*P
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 24 Avr 2012, 20:54
par loytef » 24 Avr 2012, 20:54
Joker62 a écrit:Alors tu as M la matrice de f dans les bases B_2 ; B_3
On veut la matrice M' de f dans les bases B'_2; B_3
ou B'_2 est la base canonique de R^2
Il faut donc la matrice de passage de B_2 vers B'_2. On a la note P.
On a alors
M' = M*P
Ok donc la matrice de passage P =
)
C'est correct ?
Et quelle est la différence entre ta formule M' = M*P et la formule P^-1MP ?
merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Avr 2012, 21:08
par Joker62 » 24 Avr 2012, 21:08
Oui c'est ça.
Alors ce n'est pas vraiment une différence. C'est un cas particulier surtout.
On considère une fonction f : E ----> F avec E et F deux k-ev.
On note e1 et e2 deux bases de E et f1 et f2 deux bases de F.
On note de plus A la matrice de f avec les bases e1 et f1
et B la matrice de f avec les bases e2 et f2.
On veut exprimer B en fonction de A. C'est à dire que l'on veut partir de la base e2 et arriver dans la base f2. Pour cela on va composer par des applications identités.
On note Q la matrice de l'application identité de la base e1 vers e2 (Q est donc la matrice de passage de e1 vers e2) donc Q^-1 est la matrice de passage de e2 vers e1.
Idem, on note P la matrice de l'application identité de la base f1 vers f2.
On doit partir de la base e2 et se ramener à e1 on a donc Q^- 1
On peut appliquer la matrice A qui correspond à f dans la base e1 : A
On se ramène à la base f2 en appliquant P : P
D'où B = Q^-1 * A * P
Le cas que tu cites est un cas particulier dans le sens ou on considère une application f : E --- > E
B une base de E et B' une autre base de E.
Alors si on note A la matrice de f dans B et C la matrice de f dans B' on a (en se reportant au cas général)
C = P^-1*A*P
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 25 Avr 2012, 09:51
par loytef » 25 Avr 2012, 09:51
Joker62 a écrit:Oui c'est ça.
Alors ce n'est pas vraiment une différence. C'est un cas particulier surtout.
On considère une fonction f : E ----> F avec E et F deux k-ev.
On note e1 et e2 deux bases de E et f1 et f2 deux bases de F.
On note de plus A la matrice de f avec les bases e1 et f1
et B la matrice de f avec les bases e2 et f2.
On veut exprimer B en fonction de A. C'est à dire que l'on veut partir de la base e2 et arriver dans la base f2. Pour cela on va composer par des applications identités.
On note Q la matrice de l'application identité de la base e1 vers e2 (Q est donc la matrice de passage de e1 vers e2) donc Q^-1 est la matrice de passage de e2 vers e1.
Idem, on note P la matrice de l'application identité de la base f1 vers f2.
On doit partir de la base e2 et se ramener à e1 on a donc Q^- 1
On peut appliquer la matrice A qui correspond à f dans la base e1 : A
On se ramène à la base f2 en appliquant P : P
D'où B = Q^-1 * A * P
Le cas que tu cites est un cas particulier dans le sens ou on considère une application f : E --- > E
B une base de E et B' une autre base de E.
Alors si on note A la matrice de f dans B et C la matrice de f dans B' on a (en se reportant au cas général)
C = P^-1*A*P
Bonjour,
Donc si j'ai bien compris la formule C=P^-1AP fonctionne que pour les endomorphismes.
Sinon pour la matrice g j'ai trouvé la matrice :
)
C'est correct ?
merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 25 Avr 2012, 10:47
par Joker62 » 25 Avr 2012, 10:47
Oui c'est ça.
Et la formule C = P^-1 * A * P est bien valable pour les endomorphismes (lorsque l'on utilise la même base pour le départ et l'arrivée bien sûr !). On dit d'ailleurs dans ce cas là que les matrices A et C sont semblables parce qu'elles représentent le même endomorphisme.
-
loytef
- Membre Naturel
- Messages: 63
- Enregistré le: 06 Sep 2008, 14:46
-
 par loytef » 25 Avr 2012, 11:18
par loytef » 25 Avr 2012, 11:18
Joker62 a écrit:Oui c'est ça.
Et la formule C = P^-1 * A * P est bien valable pour les endomorphismes (lorsque l'on utilise la même base pour le départ et l'arrivée bien sûr !). On dit d'ailleurs dans ce cas là que les matrices A et C sont semblables parce qu'elles représentent le même endomorphisme.
C'est ok :++:
Merci beaucoup pour ton aide Joker62
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités