Sens de variation des suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 21 Avr 2012, 13:54
par Xeniuss » 21 Avr 2012, 13:54
Bonjour à tous

Énoncé :
 http://img140.imageshack.us/img140/416/ex6j.jpg
http://img140.imageshack.us/img140/416/ex6j.jpgj'aimerai savoir si ce que j'ai fait est juste :
1)

et
}{4^{n+1}} = \frac {5n+5}{4^{n+1}})
On a


Donc la suite
)
est croissante.
La 2) je vois pas trop ce qu'il faut faire :/
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 21 Avr 2012, 14:21
par Manny06 » 21 Avr 2012, 14:21
pour la 1) je ne vois pas où est ta demonstration
calcule plutôt Un+1 -Un et etudie son signe
même méthode pour le 2)
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 21 Avr 2012, 14:28
par Xeniuss » 21 Avr 2012, 14:28
Sa donne (5n+5)/4^n+1 - (5n)/4^n mais sa c'est pour déterminer la raison non?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 21 Avr 2012, 14:45
par Manny06 » 21 Avr 2012, 14:45
Xeniuss a écrit:Sa donne (5n+5)/4^n+1 - (5n)/4^n mais sa c'est pour déterminer la raison non?
reduis tes fraction au même denominateur pour etudier le signe
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 21 Avr 2012, 14:54
par Xeniuss » 21 Avr 2012, 14:54
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 21 Avr 2012, 14:54
par M@thIsTheBest » 21 Avr 2012, 14:54
Xeniuss a écrit:Bonjour à tous

Énoncé :
 http://img140.imageshack.us/img140/416/ex6j.jpg
http://img140.imageshack.us/img140/416/ex6j.jpgj'aimerai savoir si ce que j'ai fait est juste :
1)

et
}{4^{n+1}})
= \frac {5n+5}{4^{n+1}}[/TEX]
On a


Donc la suite
)
est croissante sur IN.
La 2) je vois pas trop ce qu'il faut faire :/
}{4^{n+1}})
-

=
}{4^{n+1}})
-

=

< 0 pour tout n appartenant à IN. Donc U(n+1)<U(n): U est décroissante.
Pour la deuxième:
V(n+1)-V(n)=4n-18, Donc pour tout n

4 on a V(n+1)< V(n): V décroissante si n

4 ,sinon, pour tout n

5: V est croissante. :zen:
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 21 Avr 2012, 15:17
par Xeniuss » 21 Avr 2012, 15:17
M@thIsTheBest a écrit:}{4^{n+1}})
-

=
}{4^{n+1}})
-

=

< 0 pour tout n appartenant à IN. Donc U(n+1)<U(n): U est décroissante.
Pour la deuxième:
V(n+1)-V(n)=4n-18, Donc pour tout n

4 on a V(n+1)< V(n): V décroissante si n

4 ,sinon, pour tout n

5: V est croissante. :zen:
Pour cette étape
}{4^{n+1}})
-

on doit faire pour le nominateur

Or le n est une puissance je vois pas comment on arrive a 20n

-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 21 Avr 2012, 15:24
par Xeniuss » 21 Avr 2012, 15:24
M@thIsTheBest a écrit:}{4^{n+1}})
-

=
}{4^{n+1}})
-

=

< 0 pour tout n appartenant à IN. Donc U(n+1)<U(n): U est décroissante.
Pour la deuxième:
V(n+1)-V(n)=4n-18, Donc pour tout n

4 on a V(n+1)< V(n): V décroissante si n

4 ,sinon, pour tout n

5: V est croissante. :zen:
Oui donc V(n) est décroissante de ]-inf ; 18/4[ et croissante sur ]18/4 ; +inf[ puisque 4n-18 = 0 quand n=18/4
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 21 Avr 2012, 15:40
par Manny06 » 21 Avr 2012, 15:40
Xeniuss a écrit:Oui donc V(n) est décroissante de ]-inf ; 18/4[ et croissante sur ]18/4 ; +inf[ puisque 4n-18 = 0 quand n=18/4
n est
ENTIER tu multiplie la 2° fraction haut et bas par 4
5n/4^n= (5n*4)/(4^n)*4=20n/4^(n+1)
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 21 Avr 2012, 15:45
par Xeniuss » 21 Avr 2012, 15:45
Manny06 a écrit:n est ENTIER
tu multiplie la 2° fraction haut et bas par 4
5n/4^n= (5n*4)/(4^n)*4=20n/4^(n+1)
Ha ok merci

-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 21 Avr 2012, 18:21
par M@thIsTheBest » 21 Avr 2012, 18:21
Je n'écrie pas une démonstration pour deux fois, et j'attend un remerciement de votre part. :zen:
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 22 Avr 2012, 02:40
par Xeniuss » 22 Avr 2012, 02:40
M@thIsTheBest a écrit:}{4^{n+1}})
-

=
}{4^{n+1}})
-

=

< 0 pour tout n appartenant à IN. Donc U(n+1)<U(n): U est décroissante.
Pour la deuxième:
V(n+1)-V(n)=4n-18, Donc pour tout n

4 on a V(n+1)< V(n): V décroissante si n

4 ,sinon, pour tout n

5: V est croissante. :zen:
Mais pourquoi pas faire



D'où

Donc
)
est croissante
-
antonyme
- Membre Relatif
- Messages: 435
- Enregistré le: 28 Mar 2012, 16:07
-
 par antonyme » 22 Avr 2012, 03:42
par antonyme » 22 Avr 2012, 03:42
Xeniuss a écrit:

Salut,
Tu as confondu
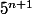
et
)
. On a en faite :

et

Donc

Ainsi
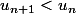
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 22 Avr 2012, 10:45
par Xeniuss » 22 Avr 2012, 10:45
antonyme a écrit:Salut,
Tu as confondu
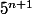
et
)
. On a en faite :

et

Donc

Ainsi
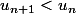
Ha oui je me suis trompé mais sa donne sa normalement
}{4^{n+1}} \times \frac {4^n}{5n})


-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 22 Avr 2012, 13:18
par Manny06 » 22 Avr 2012, 13:18
erreur
5n+5=5(n+1)
(5n+5)/5n=5(n+1)/5n=(n+1)/n
et 4^n/4^(n+1)=4^n/4^n*4=1/4
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 22 Avr 2012, 13:59
par Xeniuss » 22 Avr 2012, 13:59
Manny06 a écrit:erreur
5n+5=5(n+1)
(5n+5)/5n=5(n+1)/5n=(n+1)/n
et 4^n/4^(n+1)=4^n/4^n*4=1/4
Donc sa donne

nn?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 22 Avr 2012, 14:21
par Manny06 » 22 Avr 2012, 14:21
Xeniuss a écrit:Donc sa donne

nn?
cela donne (n+1)/4n comme te l'as écrit Antonyme
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 22 Avr 2012, 14:29
par Xeniuss » 22 Avr 2012, 14:29
Manny06 a écrit:cela donne (n+1)/4n comme te l'as écrit Antonyme
Ha autant pour moi :p en tout cas merci beaucoup a vous de m'avoir aider :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités


et

est croissante.
et
= \frac {5n+5}{4^{n+1}}[/TEX]

est croissante sur IN.
-
=
-
=
< 0 pour tout n appartenant à IN. Donc U(n+1)<U(n): U est décroissante.
4 on a V(n+1)< V(n): V décroissante si n
4 ,sinon, pour tout n
5: V est croissante. :zen:
-
=
-
=
< 0 pour tout n appartenant à IN. Donc U(n+1)<U(n): U est décroissante.
4 on a V(n+1)< V(n): V décroissante si n
4 ,sinon, pour tout n
5: V est croissante. :zen: