Question en arithmétique

par **Fan-de-Perelman** » 21 Avr 2012, 13:44

Bonjour,

j'aurai besoin d'un soutien pour la question suivante :

soit n un nombre entier naturel non nul

démontrez que

en conclure

selon les valeurs de n

pour la première question c'est évident mais pour la deuxième je vois pas comment faire...

merci d'avance pour votre aide.

par **Jota Be** » 21 Avr 2012, 14:00

Fan-de-Perelman a écrit:Bonjour,

j'aurai besoin d'un soutien pour la question suivante :

soit n un nombre entier naturel non nul

démontrez que

en conclure selon les valeurs de n

pour la première question c'est évident mais pour la deuxième je vois pas comment faire...

merci d'avance pour votre aide.

Bonjour,
Ecris la division Euclidienne de

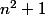
par

par **Fan-de-Perelman** » 21 Avr 2012, 14:22

ca nous donne

(n-1)(n+1)+2 mais je ne vois pas de rapport avec ce qu'on doit conclure ...

certes ca nous donne

mais il me faut une conclusion du rapport précédent

par **Jota Be** » 21 Avr 2012, 14:24

Fan-de-Perelman a écrit:ca nous donne

(n-1)(n+1)+2 mais je ne vois pas de rapport avec ce qu'on doit conclure ...

certes ca nous donne mais il me faut une conclusion du rapport précédent

Ok, et que vaut PGCD(n+1; 2) en fonction de n ?

Bon, différencie d'abord 2 cas : n=1 ou n > 1
Ensuite, pour n > 1, tu distingueras de nouveau 2 cas de figure.

par **Fan-de-Perelman** » 21 Avr 2012, 14:33

ah c'est bon on déduit le rapport que j'ai ecrit precédemment par la première question puis on en conclu par algorithme d'euclide que

en traitant le cas de

a part pour obtenir la condition de

merci

par **Fan-de-Perelman** » 21 Avr 2012, 14:34

n impair implique n+1 pair etc..

par **Jota Be** » 21 Avr 2012, 14:35

Fan-de-Perelman a écrit:n impair implique n+1 pair etc..

voilà, exact !

par **Fan-de-Perelman** » 21 Avr 2012, 15:40

comme suite de l'exercice on considère a et b deux nombres naturels tel que pgcd(a;b)=1 et

démontrez que

en conclure

pour la première question c'est bon mais je bloque à la dernière, auriez-vous une indication?
merci d'avance!

par **Fan-de-Perelman** » 21 Avr 2012, 17:18

de l'aide svp , merci :)

par **Fan-de-Perelman** » 01 Mai 2012, 18:32

par curiosité j'up ce post espérant une réponse merci :) !

par **nodjim** » 01 Mai 2012, 18:44

La division euclidienne permet de dire que n²+1=2 modulo (n+1).
PGCD(n²+1;n+1)=PGCD(n+1;2)
Si n impair, PGCD=2 si n pair PGCD=1.

par **Fan-de-Perelman** » 06 Mai 2012, 11:27

merci mais cette question a été résolue, je parlais de la dernière (le dernier message.)

Question en arithmétique

Question en arithmétique

Qui est en ligne