Suites arithmétique

[chac]

Pouvez-vous me dire si j'ai juste à cet exercice, mon résultat me parait bizarre...
Uest la suite arithmétique de raison 5 telle sue U0=2.
Il faut calculer n tel que U3+U4+...+Un=6456.
J'ai utilisé la formule: (n+1)(U0+Un)/2 ais je trouve 51873...

[maths0]

C'est une équation à résoudre alors.

[chac]

C'est une équation à résoudre alors.

On m'a conseillé d'utiliser cette formule...

[chan79]

On m'a conseillé d'utiliser cette formule...

tu as



...

Si tu ajoutes tout membre à membre

6456=2(n-2)+5( ...
Tu continues avec une équation du second degré au passage
Ca s'arrange bien

[chac]

tu as



...

Si tu ajoutes tout membre à membre

6456=2(n-2)+5( ...
Tu continues avec une équation du second degré au passage
Ca s'arrange bien

Je comprend pas l'équation qu'on obtient au final

[maths0]

Pour une suite arithmétique, pour faire la somme du premier au dernier termes on utilise la formule suivante:



Quel est le premier terme ici ? quel est le dernier ? combien il y a t'il de termes ici ?

[chac]

Pour une suite arithmétique, pour faire la somme du premier au dernier termes on utilise la formule suivante:



Quel est le premier terme ici ? quel est le dernier ? combien il y a t'il de termes ici ?

Le premier c'est U3, le dernier Un et il y a n terme c'est ça?
Donc on a (n-2)(U3+Un)/2=6456

[maths0]

Tu es d'accord on cherche n tel que: ?

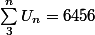
[chac]

Tu es d'accord on cherche n tel que: ?

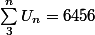
oui je suis ok

[maths0]

Combien il y a de terme en 3 et n ?

[chac]

Combien il y a de terme en 3 et n ?

Je comprend pas désolé...

[maths0]

Si on somme les termes de la suite :
De 0 à 0:
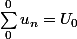
: 1 terme
De 0 à 1:
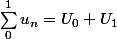
: 2 termes
De 0 à 2:
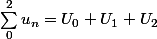
: 3 termes
De 0 à 3:
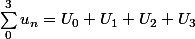
: 4 termes
De l à m:
: Combien de terme ?
De 3 à n:
: Combien de terme ?

[chac]

Si on somme les termes de la suite :
De 0 à 0:
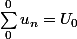
: 1 terme
De 0 à 1:
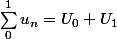
: 2 termes
De 0 à 2:
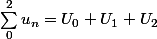
: 3 termes
De 0 à 3:
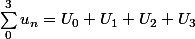
: 4 termes
De l à m:
: Combien de terme ?
De 3 à n:
: Combien de terme ?

De l à m : m-l terme
De 3 à n: n-3 termes

[maths0]

Non de l à m il y a: m-l+1 termes (dessus-bas)+1
De 3 à n il y a: ? termes

[chac]

Non de l à m il y a: m-l+1 termes (dessus-bas)+1
De 3 à n il y a: ? termes

De 3 à n: (n-3)+1

[maths0]

Oui donc en appliquant la formule ? =6456

[chac]

Oui donc en appliquant la formule ? =6456

(n-3)+1(U3+Un)/2=6456???

[maths0]

Avec Un= ? et U3 = ?

[chac]

Avec Un= ? et U3 = ?

U3=17 et Un=Uo+nr

[maths0]

(n-3)+1(U3+Un)/2=6456???

C'est fois, regarde la formule.
Tu as déjà la raison et le premier terme alors Un = ?
Au final ?