Sigma !
Réponses à toutes vos questions du CP à la 3ème
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 18 Avr 2012, 19:06
par chaa13 » 18 Avr 2012, 19:06
Moi je pense qu'il faut enlever les 2 . Si je soustrait a-b le dernier nombre serait : 1 c'est infini .
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 18 Avr 2012, 19:08
par M@thIsTheBest » 18 Avr 2012, 19:08
chaa13 a écrit:Moi je pense qu'il faut enlever les 2 . Si je soustrait a-b le dernier nombre serait : 1 c'est infini .
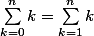
!!!!puisque le premier terme est 0 !!!! :zen:
qu'en penses tu ? :zen:
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 18 Avr 2012, 19:18
par M@thIsTheBest » 18 Avr 2012, 19:18
Øktave a écrit:Bon j'abandonne, voici la réponse ...
Dans les deux suites ont a :
(1+2) + (2+2) + (3+2) + (4+2) + (5+2) + ... + (n-2+2) + (n-1+2) + (n+2) + (n+1+2)
(0+2) + (1+2) + (2+2) + (3+2) + (4+2) + (5+2) + ... + (n-2+2) + (n-1+2) + (n+2)
Si l'on fait la premiére moins la seconde les parties colorés s'annules entre elles.
Il ne restera que (N+1+2)-(0+2)
Donc N+1+2-2=N+1
Voilà.
Mais je ne sais pas pourquoi vous compliquez les choses :zen:
J'ai mis la réponse juste en haut de la votre et de Chaa13, et je pense qu'elle est plus simple pour lui.. :zen:
-
pinocchio
- Membre Naturel
- Messages: 89
- Enregistré le: 12 Nov 2011, 22:30
-
 par pinocchio » 18 Avr 2012, 19:26
par pinocchio » 18 Avr 2012, 19:26
Autrement, Chaa, puisque maintenant tu sais écrire le sigma en TEX, tu peux faire ce genre d'exercices :
on te donne une somme de termes, il faut l'exprimer sous forme de sigma :
je pense que ceux-là ne sont pas trop compliqués :
a)

b)

c) 6+11+16+...+(5n+1)
d) 2+5+8+11+14
(en fait je trouve le d) déjà pénible :hein3:)
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 18 Avr 2012, 19:34
par chaa13 » 18 Avr 2012, 19:34
@ M@thIsTheBest et @ Øktave :
Je crois que j'ai compris ,désolé mais ...je peux essayer d'en faire un du même genre svp ,pour que je vois si j'ai bien compris !
Merci d'avance !
@pinocchio :
Pour le a)
)
Je mange et j'essaye de te faire les autres juste après .Merci !!!!!
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 18 Avr 2012, 19:39
par Jota Be » 18 Avr 2012, 19:39
M@thIsTheBest a écrit:Mais je ne sais pas pourquoi vous compliquez les choses :zen:
J'ai mis la réponse juste en haut de la votre et de Chaa13, et je pense qu'elle est plus simple pour lui.. :zen:
Je trouve que la réponse apportée par Oktave est plus évidente pour le niveau de Chaa.
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 18 Avr 2012, 20:13
par chaa13 » 18 Avr 2012, 20:13
Pour ton explication M@thIsTheBest . Quand tu a fais :
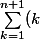-\sum_{k=0}^{n}(k))
= n+1 comment a tu fais .
Bizzare je trouve la solution d'Øktave plus simple a comprendre
-
Julie_S
- Messages: 9
- Enregistré le: 04 Avr 2012, 22:48
-
 par Julie_S » 18 Avr 2012, 20:17
par Julie_S » 18 Avr 2012, 20:17
chaa13 a écrit:Pour ton explication M@thIsTheBest . Quand tu a fais :
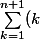-\sum_{k=0}^{n}(k))
= n+1 comment a tu fais .
Bizzare je trouve la solution d'Øktave plus simple a comprendre
Hello again

Bien, il a considéré que
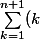-\sum_{k=0}^{n}(k)=\sum_{k=1}^{n+1}(k)-\sum_{k=1}^{n}(k))
Donc les sommes sont identiques, à l'exception près que l'on rajoute un terme n+1 pour la première somme ! D'où le résultat final. Mais cela nécessite un peu plus d'entrainement pour le voir.
Je préfère aussi la méthode d'Oktave qui est plus visuelle à ton niveau ^^
Julie
PS : je te tuerai, JB.
PPS : il est vrai aussi que l'exo que je t'avais donné à faire est plutôt
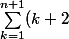-\sum_{k=0}^{n}(k+2))
!
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 18 Avr 2012, 20:20
par Jota Be » 18 Avr 2012, 20:20
Julie_S a écrit:PS : je te tuerai, JB.
On règle ça dans le jardin si tu veux, pas sur le forum :ptdr:
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 18 Avr 2012, 20:41
par chaa13 » 18 Avr 2012, 20:41
@pinocchio :
Pour d)
)
Mais c'est faux !! Car la on va partie de 5 et pas de 2 !
 par Wolstenholme » 18 Avr 2012, 20:54
par Wolstenholme » 18 Avr 2012, 20:54
Au moins tu as compris qu'on passe d'un terme à l'autre en ajoutant 3. Si on part de 2 et qu'on ajoute 3 à chaque fois alors il faut penser à séparer le 2 du reste : 2 + 3k
:livre:
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 18 Avr 2012, 21:01
par chaa13 » 18 Avr 2012, 21:01
Merci Wolstenholme
@pinocchio :
J'ai une solution pour d) avec l'aide de Wolstenholme :
)
Je vien de me rendre compte qu'il ne fallait pas mettre 14 mais 4 parce que 2 + 3*4 = 14
j'essaye la b maintenant
 par Wolstenholme » 18 Avr 2012, 21:08
par Wolstenholme » 18 Avr 2012, 21:08
chaa13 a écrit:Merci Wolstenholme
@pinocchio :
J'ai une solution pour d) avec l'aide de Wolstenholme :
)
Je vien de me rendre compte qu'il ne fallait pas mettre 14 mais 4 parce que 2 + 3*4 = 14
j'essaye la b maintenant
Oui car il y a en tout 5 termes, de façon générale (si on commence la somme avec k = 0) il y a n + 1 termes (ici n vaut 4 pour la d)
:livre:
-
pinocchio
- Membre Naturel
- Messages: 89
- Enregistré le: 12 Nov 2011, 22:30
-
 par pinocchio » 18 Avr 2012, 21:10
par pinocchio » 18 Avr 2012, 21:10
:++:
(c'est ce que je disais, je ne trouve pas la d) simple à trouver ; d'ailleurs je crois que les autres exercices de mon livre sont pires :dingue: . Les réponses sont intéressantes mais je suis obligée de regarder la correction...)
 par Wolstenholme » 18 Avr 2012, 21:12
par Wolstenholme » 18 Avr 2012, 21:12
pinocchio a écrit::++:
(c'est ce que je disais, je ne trouve pas la d) simple à trouver ; d'ailleurs je crois que les autres exercices de mon livre sont pires :dingue: . Les réponses sont intéressantes mais je suis obligée de regarder la correction...)
Montre toujours :we:
:livre:
-
chaa13
- Membre Rationnel
- Messages: 622
- Enregistré le: 25 Mar 2012, 19:52
-
 par chaa13 » 18 Avr 2012, 21:14
par chaa13 » 18 Avr 2012, 21:14
je crois avoir trouver pour b)
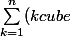)
cube représente la k exposant 3
C'est ca ?
 par Wolstenholme » 18 Avr 2012, 21:21
par Wolstenholme » 18 Avr 2012, 21:21
chaa13 a écrit:je crois avoir trouver pour b)
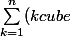)
cube représente la k exposant 3
C'est ca ?
Oui :we:
:livre:
-
pinocchio
- Membre Naturel
- Messages: 89
- Enregistré le: 12 Nov 2011, 22:30
-
 par pinocchio » 18 Avr 2012, 21:23
par pinocchio » 18 Avr 2012, 21:23
A vrai dire je n'arrive plus à trouver les exercices qui m'ont donné du mal.
Mais puisque Chaa ne va pas avoir de mal à faire la b) et la c), il y a aussi ce genre d'exercice :
"utilise la notation sigma pour écrire :
a) la somme de tous les nombres naturels à deux chiffres
b) la somme des 60 premiers nombres impairs
c) la somme de tous les nombres entre 1 et 100 inclus qui donnent un reste de 1 quand on les divise par sept"
(mais où vont-ils chercher ce genre d'énoncé ?)
ceux-là c'était à ma portée. (c'est peut-être trop simple ?)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités


= n+1 comment a tu fais .
)
