Suite de fonctions

par **Rifl3** » 15 Avr 2012, 13:21

Bonjour je bloque à la question 2 de cet exercice. :/

J'ai trouvé à la question 1 que la suite de fonction CVS vers la fonction prenant la valeur 0 sur ]0,1] et 1 en 0.
Donc il n'y a pas de CVU car la fonction n'est pas continue.
Et du coup je n'arrive pas à trouver la limite de la suite.
J'ai eu plusieurs idées mais aucune n'a aboutie. :/
Pourriez-vous me donner une indication svp?
Merci

par **girdav** » 15 Avr 2012, 13:46

On a

donc la suite converge en fait vers la fonction qui vaut 1 en 0 et 0 ailleurs. Pour la seconde partie, fixe

, et prend \delta tel que

. Il te reste à trouver majorer l'autre morceau.

par **ev85** » 15 Avr 2012, 13:47

Rifl3 a écrit:Bonjour je bloque à la question 2 de cet exercice. :/

J'ai trouvé à la question 1 que la suite de fonction CVS vers la fonction prenant la valeur 0 sur ]0,1] et exp(-1) en 0.
Donc il n'y a pas de CVU car la fonction n'est pas continue.
Et du coup je n'arrive pas à trouver la limite de la suite.
J'ai eu plusieurs idées mais aucune n'a aboutie. :/
Pourriez-vous me donner une indication svp?
Merci

Donne tes idées, même si elles n'ont pas abouti.

Tu es sûr du exp(-1) ?

par **Rifl3** » 15 Avr 2012, 14:14

ev85 a écrit:Donne tes idées, même si elles n'ont pas abouti.

Tu es sûr du exp(-1) ?

Oui, désolé c'est 1, je m'en étais rendu compte mais j'avais oublié de corrigé.
J'ai intégré par parties pour avoir du arctan(nx) mais je n'ai pas réussi a montrer non plus qu'elle CVU. Et je crois que c'est faux. J'ai essayé de prendre l'intégrale sur ]0,1] et essayé de démontrer que les fn(x) convergeait uniformément sur cet intervalle. Car pour une fonction continue par morceau l'intégrale sur ]0,1] est égale à celle sur [0,1]. Mais la fonction sur ]0,1] ne CV pas unif non plus (th d'échanges de limites en 0). J'ai aussi essayé de majorer par une suite sans succès. Et après je manquais d'idées. ^^

par **Rifl3** » 15 Avr 2012, 14:19

Par contre je viens de me rendre compte que j'ai oublié un terme en 1/n en intégrant par partie. Donc je vais réessayer. :)

par **Le_chat** » 15 Avr 2012, 15:04

Sinon, si tu l'as vu, c'est une application immédiate du théorème de convergence dominée.

par **Rifl3** » 15 Avr 2012, 16:34

Le_chat a écrit:Sinon, si tu l'as vu, c'est une application immédiate du théorème de convergence dominée.

Oui, je l'ai vu. Et oui c'est une application du th de convergence dominée, je suis vraiment parti trop loin. J'étais plutôt dans le chapitre des convergences uniforme et tout... :/. Alors que c'était vraiment bidon ^^. Merci beaucoup lol

par **ev85** » 15 Avr 2012, 16:58

Rifl3 a écrit:Oui, je l'ai vu. Et oui c'est une application du th de convergence dominée, je suis vraiment parti trop loin. J'étais plutôt dans le chapitre des convergences uniforme et tout... :/. Alors que c'était vraiment bidon ^^. Merci beaucoup lol

Sinon, à la girdav, tu te fixes

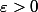
Tu as

Comme

, tu en déduis que

, et ce pour tout

.

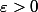
Mais bon la convergence dominée c'est le confort moderne.

par **Rifl3** » 15 Avr 2012, 17:42

Lol, merci, toute méthode est bonne à prendre. :)

Suite de fonctions

Suite de fonctions

Qui est en ligne