Montrer que pour tout entier naturel
Un problème de divisibilité
4 messages
- Page 1 sur 1
Un problème de divisibilité
Soit  la fonction qui à tout entier naturel
la fonction qui à tout entier naturel 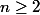 associe le plus petit entier strictement positif ayant exactement
associe le plus petit entier strictement positif ayant exactement  diviseurs distincts.
diviseurs distincts.
Montrer que pour tout entier naturel , le nombre
, le nombre ) divise
divise ) .
.
Montrer que pour tout entier naturel
i
Si on note :
 = \prod_{i=1}^k p_i^{2^{a_i}-1}) avec
avec 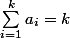 (on a forcément ce genre d'écriture car les exposants n1,...,nc doivent vérifier (n1+1)...(nc+1) = 2^k et donc n_i est une puissance de 2 moins un ; et on voit aussi très bien qu'il va falloir piocher parmi les k premiers nombres premiers).
(on a forcément ce genre d'écriture car les exposants n1,...,nc doivent vérifier (n1+1)...(nc+1) = 2^k et donc n_i est une puissance de 2 moins un ; et on voit aussi très bien qu'il va falloir piocher parmi les k premiers nombres premiers).
Si on effectue les affectations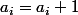 et
et 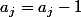 avec
avec  différent de
différent de  et
et  alors le nombre obtenu a toujours n diviseurs distincts et donc doit être supérieur à
alors le nombre obtenu a toujours n diviseurs distincts et donc doit être supérieur à) , ce qui se traduit par :
, ce qui se traduit par :

De plus, si on prend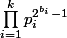 différent de
différent de) avec
avec 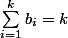 , on peut affirmer qu'il existe
, on peut affirmer qu'il existe  et
et  tels que
tels que 
Mais
Et donc le produit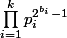 est strictement diminué par l'affectation
est strictement diminué par l'affectation 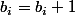 et
et 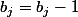 .
.
Finalement :
pour tout i différent de j, est une caractérisation de f(2^k).
est une caractérisation de f(2^k).
Mais, en considérant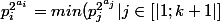) (
(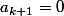) , on montre que l'affectation
, on montre que l'affectation 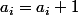 permet de passer de
permet de passer de ) à
à ) .
.
En effet, le nombre obtenu conserve la propriété enoncée :
Pour (u,v) avec u,v différent de i et k+1, c'est clair (d'après f(2^k)).
Pour (i,v) la propriété s'écrit ce qui est vrai d'après f(2^k).
ce qui est vrai d'après f(2^k).
Pour (v,i), la propriété s'écrit ce qui est vrai par minimalité.
ce qui est vrai par minimalité.
Si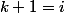 alors on a fini. Sinon
alors on a fini. Sinon 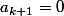 et :
et :
Pour (k+1,v) (v différent de i) la propriété s'écrit
Mais (d'après
(d'après) ) et
) et  par minimalité, ce qui prouve la propriété.
par minimalité, ce qui prouve la propriété.
Pour (v,k+1) la propriété est evidente.
Au final la propriété est vérifiée pour tout couple.
Ainsi = f(2^k}p_i^{2^{a_i}}) et donc
et donc ) divise
divise)
Ca doit pas être evident à comprendre mais ... ouf !
Si on effectue les affectations
De plus, si on prend
Mais
Et donc le produit
Finalement :
pour tout i différent de j,
Mais, en considérant
En effet, le nombre obtenu conserve la propriété enoncée :
Pour (u,v) avec u,v différent de i et k+1, c'est clair (d'après f(2^k)).
Pour (i,v) la propriété s'écrit
Pour (v,i), la propriété s'écrit
Si
Pour (k+1,v) (v différent de i) la propriété s'écrit
Mais
Pour (v,k+1) la propriété est evidente.
Au final la propriété est vérifiée pour tout couple.
Ainsi
Ca doit pas être evident à comprendre mais ... ouf !
On peut redire la même chose mais mieux.
On pose A = {p^2^k, p premier, k >=0}, et on dit que si n est un entier à 2^k diviseurs alors n se décompose en un produit de k éléments distincts de A.
Donc pour construire f(2^k) il va falloir choisir k entiers différents dans A dont le produit soit le plus petit possible. (et on oublie pour le moment qu'il y a des choix de k entiers dans A qui ne marchent pas parcequ'il y a certains entiers à prendre avant d'autres. par exemple avec {4} on obtient pas un truc à 2^1 diviseurs)
Donc naturellement on va trier A en fonction de la taille des morceaux : {2,3,4,5,7,9,11,13,16,...} et on va les prendre un par un pour construire une suite de nombres g(k). g(1) = 2, g(2) = 2*3, g(3) = 2*3*4, etc.
Comme f(2^k) est un nombre qui a 2^k diviseurs, f(2^k) est donc un produit de k éléments distincts de A donc on est sûr que g(k) <= f(2^k).
Ensuite il reste à vérifier que le g(k) qu'on a construit a bien 2^k diviseurs, et ça marche parceque la contrainte pour obtenir un nombre à 2^k diviseurs, c'est de prendre p^2^a avant p^2^b lorsque a
On pose A = {p^2^k, p premier, k >=0}, et on dit que si n est un entier à 2^k diviseurs alors n se décompose en un produit de k éléments distincts de A.
Donc pour construire f(2^k) il va falloir choisir k entiers différents dans A dont le produit soit le plus petit possible. (et on oublie pour le moment qu'il y a des choix de k entiers dans A qui ne marchent pas parcequ'il y a certains entiers à prendre avant d'autres. par exemple avec {4} on obtient pas un truc à 2^1 diviseurs)
Donc naturellement on va trier A en fonction de la taille des morceaux : {2,3,4,5,7,9,11,13,16,...} et on va les prendre un par un pour construire une suite de nombres g(k). g(1) = 2, g(2) = 2*3, g(3) = 2*3*4, etc.
Comme f(2^k) est un nombre qui a 2^k diviseurs, f(2^k) est donc un produit de k éléments distincts de A donc on est sûr que g(k) <= f(2^k).
Ensuite il reste à vérifier que le g(k) qu'on a construit a bien 2^k diviseurs, et ça marche parceque la contrainte pour obtenir un nombre à 2^k diviseurs, c'est de prendre p^2^a avant p^2^b lorsque a
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
