Voilà, je planche sur un exercice seulement j'ai vraiment du mal avec ce chapitre...
Exercice :
Soit d:
{x= -1+4t
{y= 2-t
{z= 3+t
et d' :
{x= 1+2k
{y= 6+k
{z= 8+2k
La première question consiste à montrer que les deux droites sont sécantes et donner les coordonnées de leur point d'intersection.
Après quelques calculs je trouve k=-3 et t=-1
J'ai ensuite résolu d et d' avec ces valeurs et je trouve donc I (-5 ; 3 ; 2)
La seconde question c'est là que je bloque...
Il faut déterminer l'équation cartésienne du plan P contenant d et d'.
J'ai la vague impression que c'est hyper facile mais je bloque... J'ai essayé d'obtenir un truc avec les vecteurs normaux de d et d' mais ça donne rien de vraiment convaincant...
Géométrie et plans de l'espace
10 messages
- Page 1 sur 1
antonyme a écrit:Salut,
Tu peux créer un vecteur directeurde d et un autre
de d'
Le vecteur normalau plan P contenant d et d' (non confondues) est tel que
Mais si
Il faudrait plutôt prendre le vecteur directeur du plan P dans ce cas...
drake44 a écrit:Mais siest orthogonal à
et
ça veut dire que mon plan sera orthogonal à mes droites non ?
Il faudrait plutôt prendre le vecteur directeur du plan P dans ce cas...
on te propose de trouver un vecteur n normal au plan (donc orthogonal au plan)
le plan n'a pas "un vecteur directeur"
mais puisque les deux droites D et D' sont secantes et contenues dans P en prenant un vecteur directeur de chacune on obtient une base de P
drake44 a écrit:Mais siest orthogonal à
et
ça veut dire que mon plan sera orthogonal à mes droites non ?
Il faudrait plutôt prendre le vecteur directeur du plan P dans ce cas...
Tu dois normalement savoir déterminer une équation d'un plan à partir des coordonnées d'un vecteur normal à ce plan et des coordonnées d'un point appartenant à ce plan.
Bon alors voilà ce que j'ai fais :
d:
{x= -1+4t
{y= 2-t
{z= 3+t
d' :
{x= 1+2k
{y= 6+k
{z= 8+2k
et I (-5 ; 3 ; 2), intersection des deux droites.
J'ai donc pris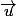 (4 ; -1 ; 1) directeur de d et
(4 ; -1 ; 1) directeur de d et 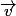 (2 ; 1 ; 2) directeur de d'.
(2 ; 1 ; 2) directeur de d'.
Ensuite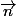 (a ; b ; c) normal à P.
(a ; b ; c) normal à P.
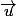 .
. 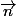 = 0 et
= 0 et 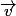 .
. 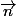 = 0
= 0
Donc on a :
{4a-b+c=0
{2a+b+2c=0
Je donne arbitrairement c=1 et après calculs je trouve a=-3/6 et b=-1.
On a donc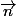 (-3/6 ; -1 ; 1).
(-3/6 ; -1 ; 1).
Par suite P : -3x/6-y+z+d=0.
J'ai injecté les coordonnées de I à l'équation pour trouver d=-3/2
Donc finalement P : -3x/6-y+z-3/2=0
Voilà j'espère que c'est ça...
d:
{x= -1+4t
{y= 2-t
{z= 3+t
d' :
{x= 1+2k
{y= 6+k
{z= 8+2k
et I (-5 ; 3 ; 2), intersection des deux droites.
J'ai donc pris
Ensuite
Donc on a :
{4a-b+c=0
{2a+b+2c=0
Je donne arbitrairement c=1 et après calculs je trouve a=-3/6 et b=-1.
On a donc
Par suite P : -3x/6-y+z+d=0.
J'ai injecté les coordonnées de I à l'équation pour trouver d=-3/2
Donc finalement P : -3x/6-y+z-3/2=0
Voilà j'espère que c'est ça...
drake44 a écrit:Bon alors voilà ce que j'ai fais :
d:
{x= -1+4t
{y= 2-t
{z= 3+t
d' :
{x= 1+2k
{y= 6+k
{z= 8+2k
et I (-5 ; 3 ; 2), intersection des deux droites.
J'ai donc pris(4 ; -1 ; 1) directeur de d et
(2 ; 1 ; 2) directeur de d'.
Ensuite(a ; b ; c) normal à P.
.
= 0 et
.
= 0
Donc on a :
{4a-b+c=0
{2a+b+2c=0
Je donne arbitrairement c=1 et après calculs je trouve a=-3/6 et b=-1.
On a donc(-3/6 ; -1 ; 1).
Par suite P : -3x/6-y+z+d=0.
J'ai injecté les coordonnées de I à l'équation pour trouver d=-3/2
Donc finalement P : -3x/6-y+z-3/2=0
Voilà j'espère que c'est ça...
ça m'a l'aire bon jusqu'à la résolution du système : avec c = 1 tu devrais trouver a=-1/2 et b=-1, mais la méthode pour trouver l'équation du plan après est bonne donc t'as juste à remplacer les valeurs :zen:
antonyme a écrit:ça m'a l'aire bon jusqu'à la résolution du système : avec c = 1 tu devrais trouver a=-1/2 et b=-1, mais la méthode pour trouver l'équation du plan après est bonne donc t'as juste à remplacer les valeurs :zen:
Certes oui :ptdr:
Petite erreur de signe qui change tout... Le d lui par contre ne change pas. Voilà ! Merci beaucoup :lol3:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
