Lois Continues

[camm]

Bonsoir,

je dois faire une raisonnement par l'absurde mais je ne comprends rien ! j'espère que quelqu'un pourra m'aider !

voici mon énoncé :

on choisit au hasard un nb réel dans l'intervalle [0;1] .
lorsque "oméga" est un ensemble fini {a1, a2, ..., an}, définir une loi de probabilité P sur "oméga" , c'est se donner les réels P({a1}), P({a2}), ..., P({an}), tous positifs ou nuls et de somme 1.
les issus devant être équiprobables, on pose, pour tout réel x de [0;1], P({x})=k avec k réel fixé. A l'évidence, k est soit nul, soit non nul ! supposons que l'on ait k 0. POur n * , on considère l'événement En= {1/n,2/n,...,n/n}.

Exprimer P(En) en fonction de k et de n, et montrer que pour n suffisamment grand, on a P(En) > 1. Que peut-on en déduire pour k ?

je sais juste que : card "oméga" = infini

merci d'avance si quelqu'un peut m'aider !

[antonyme]

supposons que l'on ait k 0. POur n *

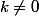
Je ne comprend pas ce passage : tu veux dire et n entier naturelle différent de 0?

[gdlrdc]

Que vaut P(En), à ton avis ?

[camm]

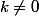
Je ne comprend pas ce passage : tu veux dire et n entier naturelle différent de 0?

ah oui excuse moi jai oublié quelques mots :/
supposons que l'on ait k 0. POur n appartient à N*

[camm]

Que vaut P(En), à ton avis ?

jai trouvé P(En) = n/k et P(En) >1 pour tt n >k

mais je suis pas du tout sûre !

[antonyme]

jai trouvé P(En) = n/k et P(En) >1 pour tt n >k

mais je suis pas du tout sûre !

Presque :lol3: P(En) = P(1/n) + P(2/n) + ... + P(n/n) = n*P({x}) = n*k
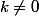
Ainsi avec et n suffisamment grand...

[gdlrdc]

oui il suffit de prendre n entier et supérieur à 1/k

[camm]

merci tous les 2:) jai compris !