Question à propos de l'écart type
79 messages
- Page 2 sur 4 - 1, 2, 3, 4
Bonjour Sylviel,
J'ai bien lu.
Un écart type égal à 0 veut bien dire que la valeur obtenue est exacte, qu'il n'y a donc pas lieu d'en refaire d'autres. Mais bizarrement, si on refait une autre mesure, par distraction, on aura alors un écart-type non nul. Comment cela peut-il se faire ?
Par ailleurs, j'ai un doute sur le sens d'espérance. Je n'ai pas trouvé de définition.
J'ai bien lu.
Un écart type égal à 0 veut bien dire que la valeur obtenue est exacte, qu'il n'y a donc pas lieu d'en refaire d'autres. Mais bizarrement, si on refait une autre mesure, par distraction, on aura alors un écart-type non nul. Comment cela peut-il se faire ?
Par ailleurs, j'ai un doute sur le sens d'espérance. Je n'ai pas trouvé de définition.
Dlzlogic a écrit: Mais bizarrement, si on refait une autre mesure, par distraction, on aura alors un écart-type non nul. Comment cela peut-il se faire ?
Par ailleurs, j'ai un doute sur le sens d'espérance. Je n'ai pas trouvé de définition.
L'écart-type n'est que la dispersion autour d'une moyenne. Si la valeur est unique, il est forcément nul. Mais s'il y a plus d'une mesure, l'écart n'en est plus un si les valeurs restent les mêmes et en devient un si elles varient, normalement.
Quant à l'espérance (moment d'ordre 1 de la v.a) : elle est la moyenne pondérée des probabilités; ceci est le résumé succint de ce que j'ai déjà fourni en guise de documents de support.
Dlzlogic a écrit:Bonjour Sylviel,
J'ai bien lu.
Un écart type égal à 0 veut bien dire que la valeur obtenue est exacte, qu'il n'y a donc pas lieu d'en refaire d'autres.
Pas du tout, l'écart type ça n'a rien à voir avec de l'exactitude ou pas. On peut définir l'écart type d'une série statistique et l'écart type d'une loi de probabilité. L'écart type d'une série statistique qui ne contient qu'une seule valeur est égal à 0, c'est trivial et ça ne veut rien dire d'autre que "un point est au même endroit que lui-même". Quant à l'écart type d'une loi de probabilité, il se calcule en connaissant la loi elle-même (et l'écart type d'une loi qui charge entièrement un singleton est nul). Si on n'a à disposition qu'un ensemble de réalisations d'une variable aléatoire qui suit la loi dont on veut calculer l'écart type, on ne peut qu'estimer l'écart type de la loi en question.
Dlzlogic a écrit:Par ailleurs, j'ai un doute sur le sens d'espérance. Je n'ai pas trouvé de définition.
Si tu commençais par lire tous les cours qu'on t'a filé, tu serais peut-être moins dans le flou. D'ailleurs, je m'étonne, le terme "espérance" apparaît dans l'énoncé du théorème central limite que tu prétends être le seul ici à comprendre. C'est marrant que tu ne comprennes pas les mots utilisés dedans...
Dites, les modos, vous allez laisser durer cette plaisanterie combien de temps encore ?
Dlzlogic a écrit:Je confond rien du tout. Une série de mesure n'a qu'un écart type.
Si on connait la valeur vraie de la moyenne, on divise par N, par exemple pour des tirages de numéros, loto, dé, etc.
Si on ne connait pas cette valeur vraie, par exemple mesure d'un longueur, alors le dénominateur est (N-1).
On ne décide pas si on connait la valeur vraie de la moyenne, on le constate.
Franchement, c'est très surprenant cette histoire de "constater que l'on connait ou pas la valeur vraie de la moyenne" et d'en déduire que l'écart type est en 1/n ou 1/(n-1).
J'aimerais bien une référence reprenant exactement ce vocabulaire et prouvant mathématiquement quelque chose concernant les 1/n et 1/(n-1)...
oh oh, je crois que je viens de comprendre ce que dit Dlzlogic !
EDIT :
laissons tomber l'écart type qui se manipule mal avec sa racine carrée, mais considérons uniquement la variance.
Comme c'est écrit ici http://fr.wikipedia.org/wiki/Estimateur_(statistique)#Estimateur_de_la_variance_de_Y
on sait que la ratio entre la variance "théorique" et celle de réalisations indépendantes est
réalisations indépendantes est 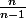 . Cela se démontre par un calcul...
. Cela se démontre par un calcul...
Notons la moyenne de la population et
la moyenne de la population et  la variance de la population.
la variance de la population.
Pour un échantillon , notons
, notons 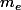 sa moyenne et
sa moyenne et 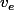 sa variance.
sa variance.
Ici, comme d'habitude,^2 }{n}) est la moyenne des carrés des différences entre les éléments de l'échantillon
est la moyenne des carrés des différences entre les éléments de l'échantillon  et sa moyenne
et sa moyenne 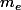 .
.
Dans cette situation, on sait que^2 }{n-1}) est un estimateur non biaisé de
est un estimateur non biaisé de  .
.
Mais ce dont parle Dlzlogic n'est pas dans ce contexte. En fait, au lieu de considérer la variance classique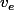 d'un échantillon
d'un échantillon  , on se met à considérer
, on se met à considérer ^2 }{n}) la moyenne des carrés des écarts entre les éléments de
la moyenne des carrés des écarts entre les éléments de  et la moyenne de la population
et la moyenne de la population  .
.
Et là, effectivement, est un estimateur non biaisé de
est un estimateur non biaisé de  !
!
En résumé, comme Dlzlogic dit à sa manière,
si on n'utilise pas la moyenne de la population, il y a
de la population, il y a  au dénominateur,
au dénominateur,
et si on utilise la moyenne de la population, il y a un
de la population, il y a un  au dénominateur...
au dénominateur...
Voir http://spiral.univ-lyon1.fr/mathsv/cours/stats/chap6/c6p4/c6p4.html , paragraphe 4.1.2.
EDIT :
laissons tomber l'écart type qui se manipule mal avec sa racine carrée, mais considérons uniquement la variance.
Comme c'est écrit ici http://fr.wikipedia.org/wiki/Estimateur_(statistique)#Estimateur_de_la_variance_de_Y
on sait que la ratio entre la variance "théorique" et celle de
Notons
Pour un échantillon
Ici, comme d'habitude,
Dans cette situation, on sait que
Mais ce dont parle Dlzlogic n'est pas dans ce contexte. En fait, au lieu de considérer la variance classique
Et là, effectivement,
En résumé, comme Dlzlogic dit à sa manière,
si on n'utilise pas la moyenne
et si on utilise la moyenne
Voir http://spiral.univ-lyon1.fr/mathsv/cours/stats/chap6/c6p4/c6p4.html , paragraphe 4.1.2.
Un écart type égal à 0 veut bien dire que la valeur obtenue est exacte, qu'il n'y a donc pas lieu d'en refaire d'autres. Mais bizarrement, si on refait une autre mesure, par distraction, on aura alors un écart-type non nul.
Et voilà, tu te places dans le cadre d'une mesure bruitée d'une valeur inconnue. Ce n'est qu'un cas particuliers et certainement pas le cas général ! Donc je reprends ce qui a été dis plein de fois :
- l'écart-type d'une variable aléatoire est un nombre qui donne une idée de la volatilité de cette variable. ie qui dis si la valeur aléatoire reste autour de son espérance ou peut s'en éloigner franchement.
- l'écart-type d'une série statistique (d'une suite de nombre quoi) donne une mesure de l'étalement de cette suite de nombre. Donc si tu as un seul nombre il n'y a pas d'étalement.
- Quand tu te places dans le cadre de la mesure tu considères une variable aléatoire (valeur exacte + bruit) dont tu disposes de plusieurs réalisations indépendantes. Cela te fournis une série statistique, mais ce que tu veux calculer ce n'est pas l'écart-type de cette série de nombre, mais l'écart-type de la variable aléatoire sous-jacente. Et pour trouver cette valeur il y a plusieurs estimateurs possible, et il se trouve qu'un estimateur sans biais est donné par la formule avec une division par n-1.
@leon : oui tu as probablement raison, en tout cas ça évoque des souvenirs ces résultats. Merci pour le rappel. Le problème de Dlzlogic est plus fondamental : c'est que pour lui toutes les probas et les stats consiste à estimer une valeur inconnue...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
"Dites, les modos, vous allez laisser durer cette plaisanterie combien de temps encore ?"
Tu vois Skullkid, faut jamais désespérer, ça discute, ça discute,
ça tourne souvent en rond,
mais il y a des moments où les fils avancent grace (à cause de) à Dlzlogic.
C'est un peu balaise pour moi, mais très intéressant, merci à Léon dont les passages-retours au forum sont appréciés!
Tu vois Skullkid, faut jamais désespérer, ça discute, ça discute,
ça tourne souvent en rond,
mais il y a des moments où les fils avancent grace (à cause de) à Dlzlogic.
C'est un peu balaise pour moi, mais très intéressant, merci à Léon dont les passages-retours au forum sont appréciés!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:"Dites, les modos, vous allez laisser durer cette plaisanterie combien de temps encore ?"
Tu vois Skullkid, faut jamais désespérer, ça discute, ça discute
Je cesserai de désespérer quand Dlzlogic daignera reconnaître ses torts (cette histoire d'écart type n'est évidemment pas le seul sujet litigieux avec lui, ça fait plusieurs mois qu'il pourrit tous les sujets de "discussion" qui lui passent sous le nez). Quand nuage a dit ce que leon1789 vient de dire (avec raison) il s'est fait rembarrer par Dlzlogic, je ne vois pas de raison d'espérer que son attitude change, il a toujours eu la même envers nuage, Sylviel, Doraki, Mathusalem, ffpower, Nightmare, toi et moi (et je dois en oublier).
Vous avez encore le courage d'essayer de ramener Dlzlogic à la raison et de modifier certains de ses dires (et d'ignorer les autres, du genre "l'écart type de la série (-1,1) est racine de 2, j'ai raison et je ne confonds rien du tout") pour leur donner du sens, j'admire, mais d'expérience, personne n'y est encore parvenu.
Sylviel a écrit:Et voilà, tu te places dans le cadre d'une mesure bruitée d'une valeur inconnue. Ce n'est qu'un cas particuliers et certainement pas le cas général ! Donc je reprends ce qui a été dis plein de fois :
- l'écart-type d'une variable aléatoire est un nombre qui donne une idée de la volatilité de cette variable. ie qui dis si la valeur aléatoire reste autour de son espérance ou peut s'en éloigner franchement.
- l'écart-type d'une série statistique (d'une suite de nombre quoi) donne une mesure de l'étalement de cette suite de nombre. Donc si tu as un seul nombre il n'y a pas d'étalement.
- Quand tu te places dans le cadre de la mesure tu considères une variable aléatoire (valeur exacte + bruit) dont tu disposes de plusieurs réalisations indépendantes. Cela te fournis une série statistique, mais ce que tu veux calculer ce n'est pas l'écart-type de cette série de nombre, mais l'écart-type de la variable aléatoire sous-jacente. Et pour trouver cette valeur il y a plusieurs estimateurs possible, et il se trouve qu'un estimateur sans biais est donné par la formule avec une division par n-1.
A ma connaissance, tous les estimateurs d'écart-type sont avec biais, y compris celui avec la division par n-1 (à cause de la racine carrée qui n'est pas propice à la moyenne).
Il y a des estimateurs sans biais de l'espérance et de la variance, mais pas pour l'écart-type. Certes, on peut essayer de minimiser le biais, mais il n'est jamais nul en toute rigueur.
Je me trompe ?
La Convergence d'estimateurs
leon1789 a écrit:Il y a des estimateurs sans biais de l'espérance et de la variance, mais pas pour l'écart-type. Certes, on peut essayer de minimiser le biais, mais il n'est jamais nul en toute rigueur.
Je me trompe ?
Des estimateurs sans biais sont préférés parce qu' ils réduisent l'erreur de la moyenne quadratique. Ceci étant dans certains cas de figure, ceux avec biais sont préférables car la convergence de var( estimateur) vers 0 est plus rapide... :lol3:
Elerinna a écrit:Des estimateurs sans biais sont préférés parce qu' ils réduisent l'erreur de la moyenne quadratique. Ceci étant dans certains cas de figure, ceux avec biais sont préférables car la convergence de var( estimateur) vers 0 est plus rapide... :lol3:
Ok.
Cela étant je ne parle pas de préférence, mais d'existence.
Il me semble qu'il n'existe pas d'estimateurs sans biais de l'écart-type (contrairement à l'espérance et à la variance) : me trompe-je ?
Shabby Louis Vuitton Purchase,Louis Vuitton Carpet-bag Cache
Louis Vuitton Bag Specialty Preserve!All Louis Vuitton Bags Factory Appoint,Much Overlook Value Off.Full Amassment Of Elevated Calibre Louis Vuitton All Items Free Shipping & Fast Transportation! louis vuitton ¥ë¥¤ ¥ô¥£¥È¥ó ¥ë¥¤¥Ó¥È¥ó
Shabby Louis Vuitton Purchase,Louis Vuitton Grip Collection,
Louis Vuitton String bag Specialty Accumulate!All Louis Vuitton Bags Factory Steer,Much Overlook Value Off.Full Collection Of High Grandeur Louis Vuitton All Items Free Shipping & Fast Delivery! louis vuitton ¥ë¥¤ ¥ô¥£¥È¥ó ¥ë¥¤¥Ó¥È¥ó
For a song Louis Vuitton Purchase,Louis Vuitton Carpet-bag R
Louis Vuitton Valise Specialty Pile up!All Louis Vuitton Bags Plant Appoint,Much Disregard Price Off.Full Collecting Of Extraordinary Calibre Louis Vuitton All Items At liberty Shipping & Sybaritically Delivery! louis vuitton ¥ë¥¤ ¥ô¥£¥È¥ó ¥ë¥¤¥Ó¥È¥ó
Shabby Louis Vuitton Mark-down,Louis Vuitton Bag Collection,
Louis Vuitton Harridan Specialty Preserve!All Louis Vuitton Bags Factory Direct,Much Ignore Expenditure Off.Full Collection Of Elevated Quality Louis Vuitton All Items At liberty Shipping & Sybaritically Transportation! louis vuitton ¥ë¥¤ ¥ô¥£¥È¥ó ¥ë¥¤¥Ó¥È¥ó
Shabby Louis Vuitton Car-boot sale,Louis Vuitton Baggage Col
Louis Vuitton String bag Specialty Store!All Louis Vuitton Bags Factory Direct,Much Disregard Price Off.Full Collection Of Elevated Quality Louis Vuitton All Items Unhampered Shipping & Fast Expression! louis vuitton ¥ë¥¤ ¥ô¥£¥È¥ó ¥ë¥¤¥Ó¥È¥ó
Cheap Louis Vuitton Sale,Louis Vuitton Baggage Store, Louis
Louis Vuitton String bag Specialty Preserve!All Louis Vuitton Bags Factory Appoint,Much Overlook Consequence Off.Full Garnering Of Elevated Quality Louis Vuitton All Items Unhampered Shipping & Closely Expression! louis vuitton ¥ë¥¤ ¥ô¥£¥È¥ó ¥ë¥¤¥Ó¥È¥ó
Train Cram Bags,Trainer Store-Nationwide Loose Shipping
Nationwide Open Shipping CARRIAGE bags,coach purse.100% real quality,fast articulation,1 week give to you! ¥³©`¥Á ز¼ ¥³©`¥Á¥Ð¥Ã¥° ¥³©`¥Á ͨØ
Train Cram Bags,Prompt Store-Nationwide Loose Shipping
Nationwide Free Shipping CRAMMER bags,coach purse.100% palpable quality,fast delivery,1 week announce to you! ¥³©`¥Á ز¼ ¥³©`¥Á¥Ð¥Ã¥° ¥³©`¥Á ͨØ
79 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
