Un petit exercice à résoudre: Montrer lexistence et donner un exemple des entiers naturels p et B tq
Arithmétique
5 messages
- Page 1 sur 1
Arithmétique
Bonjour,
Un petit exercice à résoudre: Montrer lexistence et donner un exemple des entiers naturels p et B tq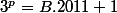
Un petit exercice à résoudre: Montrer lexistence et donner un exemple des entiers naturels p et B tq
sad13 a écrit:Comment le trouver? avec un logiciel sinon je ne vois comment; je l'ai fait avec Xcas, il a rempli la barre horizontale de chiffres
je pense qu'on doit se contenter de justifier et appliquer Fermat en mentionnant que p= 2010
Merci à vous tous, mais pour ne pas compliquer les choses :zen: on pose p=0 et B=0 et donc c'est fini !...
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
