Exercice sur une fonction longue à relation de derivation -
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 23 Mar 2012, 13:56
par DR-Youness » 23 Mar 2012, 13:56
Bonjour tous le monde , vous pouvez m'aider dans cette exercice s'il vous plait :
soit f une fonction définis sur

sous la forme :
=\sqrt{x-n}+\sqrt{x-n+1}+..+\sqrt{x}+\sqrt{x+1}+\sqrt{x+n}+..+\sqrt{x+n}-(2x+1)\sqrt{x})
1/ Montrez que f est croissante sur

2/definissez la limite quand x tend vers + de f(x) :
)
3/ on met
=\sqrt{1+x}+\sqrt{1-x}-2)
/
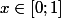
-Montrez que
\leq n\sqrt{n} ( h ( \frac{1}{n})-2))
Merci d'avance :we:
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 23 Mar 2012, 15:00
par Dlzlogic » 23 Mar 2012, 15:00
Bonjour,
Comment montre-t-on qu'une fonction est croissante sur un intervalle ?
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 23 Mar 2012, 21:04
par DR-Youness » 23 Mar 2012, 21:04
On doit calculer la dérivée puis étudier sa signe positive ou négative pour savoir si la fonction et croissante sur un 'interval ''[n;+infinie[ dans cette exercice''
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 21:11
par Judoboy » 23 Mar 2012, 21:11
h n'est pas définie sur [0;1[.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 23 Mar 2012, 21:13
par ev85 » 23 Mar 2012, 21:13
DR-Youness a écrit:Bonjour tous le monde , vous pouvez m'aider dans cette exercice s'il vous plait :
soit f une fonction définis sur

sous la forme :
=\sqrt{x-n}+\sqrt{x-n+1}+..+\sqrt{x}+\sqrt{x+1}+\sqrt{x+n}+..+\sqrt{x+n}-(2x+1)\sqrt{x})
1/ Montrez que f est croissante sur

2/definissez la limite quand x tend vers + de f(x) :
)
3/ on met
=\sqrt{x+1}+\sqrt{x-1}-2)
/

-Montrez que
\leq n\sqrt{n} ( h ( \frac{1}{n})-2))
Merci d'avance :we:
ça ne serait pas
=\sqrt{x-n}+\sqrt{x-n+1}+..+\sqrt{x}+\sqrt{x+1}+\sqrt{x+n}+..+\sqrt{x+ n}-(2n+1)\sqrt{x})
des fois ?
e.v.
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 23 Mar 2012, 21:32
par DR-Youness » 23 Mar 2012, 21:32
Je suis sur Messieurs tous les conditions d'exercices sont validés
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 21:43
par Judoboy » 23 Mar 2012, 21:43
Ok donc ça te pose pas de problème de définir racine(x-1) sur [0;1] ?
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 23 Mar 2012, 21:45
par DR-Youness » 23 Mar 2012, 21:45
c'est un probléme mais c'est les conditions je peux rien faire si je compris je vais deja esseyer de resoudre l'exercice ^^'
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 21:49
par Judoboy » 23 Mar 2012, 21:49
Nan mais te lance pas là-dedans comme ça, l'énoncé est faux...
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 23 Mar 2012, 21:56
par DR-Youness » 23 Mar 2012, 21:56
Ok désoler mais vous pouvez m'aider pour les premiere questions soyer sur que je vais discuter avec le prof sur ca :D
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 24 Mar 2012, 13:59
par DR-Youness » 24 Mar 2012, 13:59
J'ai rien compris , mais j'ai régler le probléme de h
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 24 Mar 2012, 15:07
par Judoboy » 24 Mar 2012, 15:07
Il reste le problème de f, c'est sûrement comme l'a fait remarquer ev85 un terme en (2n+1)*racine(x) en dernier, car telle que tu l'as écrite ta fonction tend vers - l'infini en quand x tend vers + l'infini et elle ne peut donc pas être décroissante.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 24 Mar 2012, 15:47
par ev85 » 24 Mar 2012, 15:47
Judoboy a écrit:Il reste le problème de f, c'est sûrement comme l'a fait remarquer ev85 un terme en (2n+1)*racine(x) en dernier, car telle que tu l'as écrite ta fonction tend vers - l'infini en quand x tend vers + l'infini et elle ne peut donc pas être décroissante.
En tout cas, MA fonction f (à moi que j'ai) elle est croissante, elle, nananère !
e.v.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 24 Mar 2012, 15:58
par Judoboy » 24 Mar 2012, 15:58
J'ai fait une coquille, je voulais dire "elle ne peut pas être croissante", telle que DR-Youness l'a donnée. La tienne avec le (-2n+1)racine(x) est sûrement croissante, je veux bien te croire.
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 24 Mar 2012, 19:44
par DR-Youness » 24 Mar 2012, 19:44
Eih j'ai rien compris moi aussi ):

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Mar 2012, 20:44
par chan79 » 24 Mar 2012, 20:44
ev85 a écrit:ça ne serait pas
=\sqrt{x-n}+\sqrt{x-n+1}+..+\sqrt{x}+\sqrt{x+1}+\sqrt{x+n}+..+\sqrt{x+ n}-(2n+1)\sqrt{x})
des fois ?
e.v.
oui, avec (2x+1), f n'est pas croissante
c'est vite fait de tracer la courbe avec n=3 par exemple
-
DR-Youness
- Membre Naturel
- Messages: 11
- Enregistré le: 26 Fév 2012, 11:21
-
 par DR-Youness » 24 Mar 2012, 21:26
par DR-Youness » 24 Mar 2012, 21:26
c'est trop compliqué
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 26 Mar 2012, 12:00
par ev85 » 26 Mar 2012, 12:00
DR-Youness a écrit:c'est trop compliqué
Qu'est-ce qui est compliqué ? De donner un énoncé exact ?
[Edit] On est passé à l'heure d'été sur ce forum ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
sous la forme :
=\sqrt{x-n}+\sqrt{x-n+1}+..+\sqrt{x}+\sqrt{x+1}+\sqrt{x+n}+..+\sqrt{x+n}-(2x+1)\sqrt{x})
)
/

\leq n\sqrt{n} ( h ( \frac{1}{n})-2))