Intersection d'hyperplan

[ilsraa]

La question est:

Soit H1 et H2 deux hyperplans d’un ;)-espace vectoriel de dimension finie. Trouver la dimen-
sion de H1 ;) H2 .


J'ai trouvé

Dim(H1 ;) H2 )=Dim(H1)+Dim(H2)-Dim(n)
où n est la dimension du ;)-espace vectoriel.
Est-ce vraie?
Et si non, comment pourrais je résoudre correctement l'exercise?
Merci

[Judoboy]

Je dis n'importe quoi, je devrais pas poster quand je suis aussi crevé.

[yos]

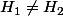
C'est juste pourvu que . C'est la formule de Grassmann compte tenu du fait que .
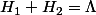
Il faut écrire et pas .
Il faut aussi pousser le calcul jusqu'au bout...

[ilsraa]

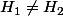
C'est juste pourvu que . C'est la formule de Grassmann compte tenu du fait que .
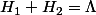
Il faut écrire et pas .
Il faut aussi pousser le calcul jusqu'au bout...

Je pensais avor déjà poussé le calcul jusqu'au bout.
Donc ici on a deux cas a étudier.
cas1: H1=H2
cas2: H1=!H2

C'est bien ça?

Pourrais tu me donner un petit coup de pousse s'il te plais!

[yos]

Donc ici on a deux cas a étudier.
cas1: H1=H2
cas2: H1=!H2

Le premier cas est trivial mais il faut le signaler.

Je pensais avor déjà poussé le calcul jusqu'au bout.

Ben non, ...

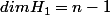
[ilsraa]

Le premier cas est trivial mais il faut le signaler.


Ben non, ...

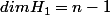
donc on a:

cas 1: dim H1=dim H2
Donc l'intersection est 0?

cas 2: dim H1=n-1
dim H2=n-1

Intersection n-(n-1+n-1)=-n + 2
?

[yos]

cas 1: dim H1=dim H2

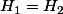
Evidemment qu'ils ont même dimension, c'est des hyperplans. Le cas 1 c'est et l'intersection de deux ensembles égaux c'est pas 0 ni le vide, c'est l'ensemble en question.

Quant au calcul final, je ne sais que te dire. Une dimension négative ça ne te pose pas de problème apparemment.

[ilsraa]

Ok j'ai compris pour le cas 1.
Oui je suis bete si n etait superieur a 0, on aurai un problème.

H1 a une dimension de n-1 et H2 a une dimension de n-1, dans le cas ou H1=!H2, on a au minimum une dimension de (n-1)+(n-1)-n=n-2
Or si n est inferieur a 2 on a un problème, c'est bien ça?
Merci

[yos]

dans le cas ou H1=!H2, on a au minimum une dimension de (n-1)+(n-1)-n=n-2

"au minimum" est de trop.

si n est inferieur a 2 on a un problème, c'est bien ça?

Si n=1, le 2ème cas ne peut pas se produire.

[ilsraa]

"au minimum" est de trop.


Si n=1, le 2ème cas ne peut pas se produire.

Ah oui, car si n=1
dim(H1) et dim(H2) sont 0!!
Merci