Lim (sinx-x)/x^3 lorsque x tend vers 0
Et merci :we:
Une limite a couper le souffle...
12 messages
- Page 1 sur 1
Travaillons tout d'abord sur l'intervalle 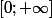
 \le 1)
-x \le 1-x)
-x}{x^3} \le \frac{1-x}{x^3}) (car
(car  supérieur à 0 sur
supérieur à 0 sur 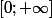 )
)
Or:
=\lim_{x\rightarrow 0^-}(\frac{-x}{x^3})) (limite d'une fonction rationnelle)
(limite d'une fonction rationnelle)
=\lim_{x\rightarrow 0^-}(\frac{-1}{x^2}))
=-\infty) (car x² tend vers
(car x² tend vers  en 0)
en 0)
Enfin, comme-x}{x^3} \le \frac{1-x}{x^3}) , par comparaison de limite, on en déduit donc que:
, par comparaison de limite, on en déduit donc que:
-x}{x^3})=- \infty)
=- \infty)
De plus,=\frac{sin(x)-x}{x^3}) .
.
Donc=\frac{sin(-x)-(-x)}{(-x)^3})
=\frac{-sin(x)+x}{-x^3})
=\frac{-(sin(x)-x)}{-x^3})
=\frac{sin(x)-x}{x^3})
=f(x))
On en déduit donc que f(x) est paire.
Or, comme=- \infty) . De par la parité de f(x), on en déduit que:
. De par la parité de f(x), on en déduit que:
=- \infty)
Ainsi:
=- \infty)
:we:
Or:
Enfin, comme
De plus,
Donc
On en déduit donc que f(x) est paire.
Or, comme
Ainsi:
:we:
sur ]0,1]
-x}{x^3} \leq x^2 - \frac{1}{6}) equivaut a
equivaut a
x^3 + x - sin(x)) (notée f)
(notée f)
si tu montre que cette expression est positive linterval alors tu demontres la premier inegalite ( la seconde etant-x}{x^3} \geq -x^2 - \frac{1}{6}) )
)
Pour cela tu peux par exemple deriver derivé 3 fois et conclure que 'f' est croissante, par prolongement elle admet donc un minimum en 0 lequel vaut 0, tu as donc bien
-x}{x^3} \leq x^2 - \frac{1}{6})
de la meme facon tu aurais montré la seconde inegalité
tu as donc
-x}{x^3} \leq x^2 - \frac{1}{6})
On utilise alors le th des gendarmes, et lon conclut que la limite de
-x}{x^3}) en 0 ( par valeure superieure ) vaut -1/6 :happy3:
en 0 ( par valeure superieure ) vaut -1/6 :happy3:
si tu montre que cette expression est positive linterval alors tu demontres la premier inegalite ( la seconde etant
Pour cela tu peux par exemple deriver derivé 3 fois et conclure que 'f' est croissante, par prolongement elle admet donc un minimum en 0 lequel vaut 0, tu as donc bien
de la meme facon tu aurais montré la seconde inegalité
tu as donc
On utilise alors le th des gendarmes, et lon conclut que la limite de
salut!
oui on peut utiliser les encadrements dans ce cas ( N.B: sin x =sigma(k de1àl'infini) (-1)^k(x^2k+1)/(2k+1)! : alors pour l'encadrer on s'arrête sur les moins du côté infirieur et sur les plus de l'autre côté ) mais aussi on peut utiliser le théorème de l'hôpital (qu'on peut démontrer)
le théorème est le suivant: soit f et g deux fonctions dérivables n fois sur IR et f(x0)=g(x0) alors lim (x--->x0) f(x)/g(x) = lim (x--->x0) f'(x)/g'(x) = lim (x--->x0) f"(x)/g"(x)=....
oui on peut utiliser les encadrements dans ce cas ( N.B: sin x =sigma(k de1àl'infini) (-1)^k(x^2k+1)/(2k+1)! : alors pour l'encadrer on s'arrête sur les moins du côté infirieur et sur les plus de l'autre côté ) mais aussi on peut utiliser le théorème de l'hôpital (qu'on peut démontrer)
le théorème est le suivant: soit f et g deux fonctions dérivables n fois sur IR et f(x0)=g(x0) alors lim (x--->x0) f(x)/g(x) = lim (x--->x0) f'(x)/g'(x) = lim (x--->x0) f"(x)/g"(x)=....
inutile ici de partir dans des encadrements : le plus simple est d'écrire le développement limité du sinus à l'ordre 3 en 0 :
sin(x) = x - ((x^3)/6) + o((x^3)) ( x -> 0 )
( meilleur polynome approchant le sinus en 0 à l'ordre 3 )
d'ou directement :
(sin(x)-x)/(x^3)) = -1/6 + o(1) ( x -> 0 )
on retrouve bien cette limite de -1/6 en 0 .
sin(x) = x - ((x^3)/6) + o((x^3)) ( x -> 0 )
( meilleur polynome approchant le sinus en 0 à l'ordre 3 )
d'ou directement :
(sin(x)-x)/(x^3)) = -1/6 + o(1) ( x -> 0 )
on retrouve bien cette limite de -1/6 en 0 .
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
