Suite croissante

par **Ellyrius** » 17 Mar 2012, 15:01

Bonjour à tous, je viens vers vous pour obtenir ma réponse a ma question car après de nombreuse heures de recherche je n'ai toujours pas réussi...

Ma question :
Comment puis-je démontrer que la suite Un définie pour tout n supérieur à 3 par Un=(n/2)sin(360/n) est croissante ?

J'aimerai une réponse ne se basant que sur les outils disponible en Ts si cela est possible

Cordialement, Merci d'avance.

par **Iroh** » 17 Mar 2012, 15:29

Bonjour,

D'abord, quelle est la définition d'une suite croissante ?
Et si on pose

, pour

, quelles valeurs peut prendre

? (dans quelle intervalle ?)

par **Ellyrius** » 17 Mar 2012, 16:23

J'ai déjà fait tout ça mais je parviens pas a le démontrer que ce soit en passant par le quotient ou la différence de deux termes consécutifs...

sin(360/n)/sin(360/n-1) est inférieur a 1
et n/n-1 est supérieur a 1

Âpres je vois pas comment faire...

par **Iroh** » 17 Mar 2012, 16:33

On ne peut pas donner des réponses toute faite, seulement guider le raisonnement.
Soit

.

est une suite croissante si

. C-à-d ici:

.

Q1: Si on pose

, quelles valeurs peut prendre

, dans quelle intervalle? (en n'oubliant pas que n > 3).

par **Ellyrius** » 17 Mar 2012, 16:38

le sinus est + puissue 360/n appartient à [0;90]

par **chan79** » 17 Mar 2012, 16:51

Ellyrius a écrit:le sinus est + puissue 360/n appartient à [0;90]

salut
c'est bien sin(360°/n) c'est-à-dire sin(2pi/n) ????

par **Ellyrius** » 17 Mar 2012, 16:52

chan79 a écrit:salut
c'est bien sin(360°/n) c'est-à-dire sin(2pi/n) ????

c'est bien cela

par **chan79** » 17 Mar 2012, 18:00

Ellyrius a écrit:c'est bien cela

je ne sais pas si c'est la méthode attendue mais ça peut se faire en montrant que la fonction
f(x)=(x/2)*sin(2pi/x) est croissante sur [4,+inf[
on calcule la dérivée
c'est un peu long mais pas difficile

par **Ellyrius** » 17 Mar 2012, 18:26

tu veux dériver le produit d'un fonction et la composée d'une composée ?

Certainement trop long n'y a t-il rien de plus simple ?

par **chan79** » 17 Mar 2012, 19:02

Ellyrius a écrit:tu veux dériver le produit d'un fonction et la composée d'une composée ?

Certainement trop long n'y a t-il rien de plus simple ?

f(x)=

f'(x)=

C'est pas si terrible, en TS :we:
il faut montrer que cette dérivée est toujours positive
si x>4 le cosinus est positif, tu divises par ce cosinus
il faut ensuite redériver
on te proposera peut-être plus simple
Bon courage

par **Ellyrius** » 17 Mar 2012, 19:12

chan79 a écrit:f(x)=
f'(x)=
C'est pas si terrible, en TS :we:
il faut montrer que cette dérivée est toujours positive
si x>4 le cosinus est positif, tu divises par ce cosinus
il faut ensuite redériver
on te proposera peut-être plus simple
Bon courage

x est différent de 0 tu peux simplifier par x et par 2

par **chan79** » 17 Mar 2012, 19:58

Ellyrius a écrit:x est différent de 0 tu peux simplifier par x et par 2

Bien-sûr, ça s'arrange assez bien.
Je te suggère de continuer le calcul, même si finalement, tu le feras d'une autre façon

par **Ellyrius** » 17 Mar 2012, 20:24

Ben merci mais ça me parait beaucoup trop long...

Si quelqu'un a d'autre idées...

par **chan79** » 17 Mar 2012, 20:41

Ellyrius a écrit:Ben merci mais ça me parait beaucoup trop long...

Si quelqu'un a d'autre idées...

sinon, calcule u(n+1)-u(n)

par **Ellyrius** » 17 Mar 2012, 20:59

chan79 a écrit:sinon, calcule u(n+1)-u(n)

essaye mais je débouche sur rien...

par **Joker62** » 17 Mar 2012, 21:56

Hello !

On considère le cercle trigonométrique et le point A de coordonnées (1,0);

Alors pour n >= 4, on construit le polygone régulier à n côtés.
Ce polygone régulier est constitué de n triangles identiques.

Calculons l'aire d'un de ces triangles. (Par exemple en prenant OAB avec B le point du cercle tel que (OA;OB) = 2;)/n rad)

On utilise la formule base*hauteur/2.

ça tombe bien : base = 1 et Hauteur = sin(360/n)

Au final, l'aire du polygone régulier est donc n*sin(360/n)/2 = u_n

Plus n est grand, plus le polygône devient proche du cercle unité et plus son aire se rapproche de l'aire du disque de façon croissante.

Bien sûr, ça reste assez heuristique :)

par **chan79** » 17 Mar 2012, 22:25

Joker62 a écrit:Hello !

On considère le cercle trigonométrique et le point A de coordonnées (1,0);

Alors pour n >= 4, on construit le polygone régulier à n côtés.
Ce polygone régulier est constitué de n triangles identiques.

Calculons l'aire d'un de ces triangles. (Par exemple en prenant OAB avec B le point du cercle tel que (OA;OB) = 2;)/n rad)

On utilise la formule base*hauteur/2.

ça tombe bien : base = 1 et Hauteur = sin(360/n)

Au final, l'aire du polygone régulier est donc n*sin(360/n)/2 = u_n

Plus n est grand, plus le polygône devient proche du cercle unité et plus son aire se rapproche de l'aire du disque de façon croissante.

Bien sûr, ça reste assez heuristique

Bien vu
Il y a une autre approche
n/2 sin(2pi/n)= pi* n/(2pi)sin(2pi/n)= pi * (sin(2pi/n))/(2pi/n)
la limite de la fraction est 1 (sinx/x tend vers 1 qd x tend vers 0)
donc la suite converge vers pi

par **Iroh** » 17 Mar 2012, 22:25

Ça prend environs une page analytiquement en étudiant la fonction

.

J'ne vais pas mettre tous les détails:

Étude de

:

D'où pas de racine pour

pour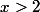

On regarde g'(x) en une valeur de x > 2, on voit que g'(x) 2. De plus on remarque que

donc g(x) est positive pour x > 3; d'où

pour x > 3, on remarque qu'elle est positive pour x > 3, d'où f(x) est croissante pour x > 3.

par **Ellyrius** » 17 Mar 2012, 22:29

merci a tout les deux je sais déjà tout ça en effet pour tout n supérieur a 3 on a :

(n/2).sin(360/n)
mais ce que j'essaye de faire démontrer que les deux suites sont croissante/décroissante, minorée/majorée, convergentes et adjacente

je sais qu'elles le sont mais mon but c'est d'essayer de le démontrer ce n'est pas pour un DM, ni pour un contrôle ni pour un exo donner par le prof, juste pour ma culture personnelle

Alors si quelqu'un a la solution s'il pouvait la donner se serait plaisant

Cordialement

par **chan79** » 18 Mar 2012, 07:50

Ellyrius a écrit:merci a tout les deux je sais déjà tout ça en effet pour tout n supérieur a 3 on a :

(n/2).sin(360/n)<pi<n.tan(180/n)

mais ce que j'essaye de faire démontrer que les deux suites sont croissante/décroissante, minorée/majorée, convergentes et adjacente

je sais qu'elles le sont mais mon but c'est d'essayer de le démontrer ce n'est pas pour un DM, ni pour un contrôle ni pour un exo donner par le prof, juste pour ma culture personnelle

Alors si quelqu'un a la solution s'il pouvait la donner se serait plaisant

Cordialement

pour la croissance de u(n), je crois qu'on t'a donné la réponse ....
Iroh te l'a détaillée un peu plus que moi
pour v(n)=n*tan(pi/n) on peut procéder de façon analogue
Par ailleurs, pense éventuellement au théorème des gendarmes pour les suites

Suite croissante

suite croissante

Qui est en ligne