équation fonctionnelle

par **egan** » 07 Mar 2012, 08:33

Salut tout le monde,

J'ai trouvé une équation fonctionnelle sympa:

Soit f de

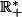
dans lui même telle que:

et dont la limite en 0 est plus l'infini.

La première étape, c'est de montrer que f est involutive. J'en suis là moi:

Il faut donc que je montre que f(1)=1 mais je ne dispose que de f(f(1))=f(1).

Si vous avez des idées, je suis preneur.
Merci d'avance.

@+ Boris.

par **ffpower** » 07 Mar 2012, 11:23

Notant a=f(1) tu as f(a)=a

Prenant x=1, y=a t'obtiens a=a²

par **egan** » 07 Mar 2012, 12:39

ffpower a écrit:Notant a=f(1) tu as f(a)=a

Prenant x=1, y=a t'obtiens a=a²

Merci. C'est malin ce que tu as fait. Avec ça, on prouve que f est involutive et ensuite que f conserve le produit.
Je pense que f est continue. Si j'arrive à montrer ça, c'est quasiment fini mais je ne vois pas comment m'y prendre. Et puis surtout, je ne vois absolument pas comment exploiter la limite, ce qui est embêtant.

par **ffpower** » 07 Mar 2012, 17:57

Note que si x>1, x^n tend vers l'infini quand n tend vers l'infini

par **egan** » 08 Mar 2012, 12:25

ffpower a écrit:Note que si x>1, x^n tend vers l'infini quand n tend vers l'infini

En utilisant ton indication, j'ai montré que f était décroissante. Mais je bloque toujours pour la continuité.
Je viens aussi de me rendre compte qu'il suffit de montrer qu'elle est continue en 1 pour qu'elle soit continue partout. En fait, continue en au moins un point suffit.

par **egan** » 09 Mar 2012, 08:07

Une autre petite indication pour la continuité ? :help: ^^

par **ffpower** » 09 Mar 2012, 13:17

Inutile de montrer la continuité, la monotonie permet de s'en passer.
ps: f m'a plutôt l'air croissante que décroissante

par **egan** » 09 Mar 2012, 13:33

ffpower a écrit:Inutile de montrer la continuité, la monotonie permet de s'en passer.
ps: f m'a plutôt l'air croissante que décroissante

La limite de f en 0 est plus l'infini. Elle ne peut donc pas croître.

Comment tu comptes t'y prendre par contre pour conclure uniquement avec la monotonie ?

par **ffpower** » 09 Mar 2012, 16:45

Ah oui j'avais pas fait gaffe que c'était la limite en 0..

Pour conclure avec la monotonie, bah c'est presque pareil que pour conclure avec la continuité (tu n'as jamais fait l'équa fonctionnelle "f(x+y)=f(x)+f(y) et f(xy)=f(x)f(y)"?)

Tu en es où pour l'instant? tu as déterminé f sur un ensemble dense?

par **egan** » 10 Mar 2012, 13:21

Je sais faire ces équations fonctionnelles si f est continue mais je ne vois pas comment faire si f est décroissante.

par **ffpower** » 10 Mar 2012, 13:30

Tu ne saurais pas par exemple montrer que si une fonction croissante f sur R vérifie f(x)=x pour tout x dans Q alors elle vérifie en fait f(x)=x pour tout x dans R?

par **egan** » 10 Mar 2012, 13:33

Si ça je pense que je sais faire mais c'est plutôt le fait d'obtenir une égalité sur Q qui me gêne.

par **ffpower** » 10 Mar 2012, 15:14

Bah ça n' a pas vraiment de rapport avec la continuité ce passage..

Bon, imaginons qu'on rajoute l'hypothèse "f est continue" dans ton équation fonctionnelle: comment tu fais pour la résoudre?

par **egan** » 11 Mar 2012, 12:04

Je montre le résultat sur Q et je finis par densité et continuité.
Je viens de comprendre ce que je comprennais pas. Merci je vais essayer de mettre ça en forme.

par **Matt_01** » 12 Mar 2012, 18:08

J'ai l'impression qu'une fois qu'on a la décroissance stricte c'est assez simple en fait :
x -> x est croissante sur R*+ et f décroissante : f admet un unique point fixe qui est 1.
Or pour x = y dans la première equation, on a xf(x) point fixe pour tout x : xf(x)=1.

par **ffpower** » 12 Mar 2012, 18:35

Pas faux :++:

par **Bony** » 12 Mar 2012, 19:32

f est involutive donc par conséquent ne peut etre que strictement croissante ou strictement décroissante ... à priori strictement croissante me parait difficile si f tend vers + infini en 0 donc f est strictement décroissante. Apres la solution est au dessus

par **ffpower** » 12 Mar 2012, 20:30

Ca par contre c'est faux sans hypothèse de continuité

par **Bony** » 12 Mar 2012, 20:59

oui avec continuité bien sur

par **Matt_01** » 13 Mar 2012, 18:15

En fait j'ai trouvé ma solution car je ne trouvais pas celle que tu proposais ffpower.
Après reflexion, tu veux montrer que f(x^s)=f(x)^s pour tout s et conclure que f est une puissance de l'identité ?

équation fonctionnelle

équation fonctionnelle

Qui est en ligne