Calcul d'un PGCD

[euler21]

Bonjour
dans un exercice on s'est donné un polynôme P de Q[X] unitaire, et le ppcm des dénominateurs des coefficients de P.
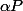
Si je pose le pgcd des coefficients du polynôme (qui appartient à Z[X]). Est ce qu'on a ??
Merci pour vos réponses

[Judoboy]

Ca doit pouvoir se faire par récurrence sur le degré de P, mais j'aime bien par l'absurde. Que peut-on dire si on suppose que c(alpha*P) est différent de 1 ?

Au fait ça ne marche que si tu as bien pris des fractions irréductibles pour ton écriture de P(X).

[leon1789]

si on prend P = 2/3 X + 2/5 ??

[euler21]

si on prend P = 2/3 X + 2/5 ??

On ne peut prendre ce cas car P doit être unitaire

[leon1789]

On ne peut prendre ce cas car P doit être unitaire

argh, pas vu... trop vite lu.
C'est ok alors !


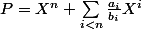
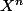
avec (avec un 1 de :lol3: )

Une idée (sans récurrence, sans absurde) :
considérer un diviseur d commun à tous les numérateurs
Alors ce diviseur d est premier avec tous les ...

[euler21]

argh, pas vu... trop vite lu.
C'est ok alors !


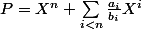
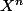
avec (avec un 1 de :lol3: )

Une idée (sans récurrence, sans absurde) :
considérer un diviseur d commun à tous les numérateurs
Alors ce diviseur d est premier avec tous les ...

je ne pense pas que c'est suffisant, d'autant qu'on multiplie tous les par ...

[euler21]

Personnellement je pense que je vais utiliser une méthode par l'asurde:
je suppose que >1 et donc il admet au moins un diviseur premier noté
Ce diviseur premier divise (P est unitaire ...) et divise aussi .
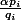
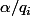
En remarquant que est un entier
On a nécessairement p divise ou p divise .
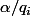
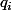
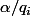
Si p divise alors p est premier avec . Si on suppose aussi que p est premier avec alors p sera premier avec ce qui est absurde.
Ainsi on a nécessairement dans tous les cas p divise ...
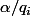
Je pense que ceci permet de conclure en utilisant la décomposition en facteurs premiers de
Edit: je m'étais trompé dans la notation maintenant je pense que c'est plus correct

[Judoboy]

Personnellement je pense que je vais utiliser une méthode par l'asurde:
je suppose que >1 et donc il admet au moins un diviseur premier noté
Ce diviseur premier divise (P est unitaire ...) et divise aussi .

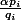
Ah bon pourquoi ? Pi/Qi n'a aucune raison d'être entier...

[ffpower]

Je pense qu'il voulait plutôt prendre p un diviseur du pgcd

[euler21]

Je pense qu'il voulait plutôt prendre p un diviseur du pgcd

Oui c'est ça je viens de modifier ma réponse, merci pour la remarque :lol3:

[Judoboy]

Ok , pour conclure il te reste juste à voir que si p divise alpha/Qi, tous les Qi divisent alpha/p, je te laisse trouver la contradiction :)

[Maxmau]

Ok , pour conclure il te reste juste à voir que si p divise alpha/Qi, tous les Qi divisent alpha/p, je te laisse trouver la contradiction

Bj autre méthode
je note Ai/Bi le coeff de X^i (i < n) ds le polynôme P
M le ppcm des Bi , M = Bi Mi
Ai et Bi premiers entre eux d'où Bezout : AiUi + BiVi = 1 et (AiMi)Ui + MVi = Mi
tout diviseur commun à M et aux AiMi divise donc Mi
les Mi sont premiers entre eux (th d'arithmétique)
donc M et les AiMi sont premiers entre eux

[euler21]

Ok , pour conclure il te reste juste à voir que si p divise alpha/Qi, tous les Qi divisent alpha/p, je te laisse trouver la contradiction

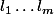
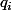
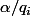
Pour la contradiction j'ai opté plutôt pour la décomposition de en produit de facteurs premiers: p étant un diviseur premier, alors p est nécessairement l'un de ces facteurs . Or étant le ppcm des , on peut toujours trouver un indice pour que ne contient pas dans sa décomposition le nombre premier
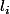
ainsi p n'est égal à aucun facteur premier de la décomposition de contradiction