Raisonnement par récurence avec factorielle

[thomas-buz]

Bonjours,
alors j'ai une démonstration par récurrence à faire:
Montrez que pour tout k appartenant à N*
k!>= 2^(k-1)

Mais je ne vois pas comme rédigez celà

[globule rouge]

Bonjours,
alors j'ai une démonstration par récurrence à faire:
Montrez que pour tout k appartenant à N*
k!>= 2^(k-1)

Mais je ne vois pas comme rédigez celà

Salut =)
Commençons par le début : à l'initialisation, il est clair que
Donc la propriété est vraie au premier rang.

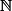
Maintenant, on veut prouver que si elle est vraie pour un certain n de , alors elle sera vraie au rang suivant .
Commençons par supposer que
or , donc...

[thomas-buz]

Salut =)
Commençons par le début : à l'initialisation, il est clair que
Donc la propriété est vraie au premier rang.

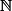
Maintenant, on veut prouver que si elle est vraie pour un certain n de , alors elle sera vraie au rang suivant .
Commençons par supposer que
or , donc...

donc (k+1)k!>2^(k-1)*(k+1)
donc (k+1)!>2k* (k+1)/2 ?

[globule rouge]

donc (k+1)k!>2^(k-1)*(k+1)
donc (k+1)!>2k* (k+1)/2 ?

ton écriture à la deuxième ligne pour le deuxième membre n'est pas très claire... dis-tu ou ?
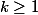
En tout cas, notre but est de montrer que donc il nous suffit de remarquer que puisque =p

[thomas-buz]

ton écriture à la deuxième ligne pour le deuxième membre n'est pas très claire... dis-tu ou ?
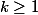
En tout cas, notre but est de montrer que donc il nous suffit de remarquer que puisque =p

Je voulais dire la premiere écriture mais c'est vrai que ta manière est plus facile
je ne vois pas comment faire après
a pars si je fais
(k+1)k!>= 2^k k! >= 2^k/ (k+1)
Nan j'vois pas en faite lol

[globule rouge]

Je voulais dire la premiere écriture mais c'est vrai que ta manière est plus facile
je ne vois pas comment faire après
a pars si je fais
(k+1)k!>= 2^k k! >= 2^k/ (k+1)
Nan j'vois pas en faite lol

non non non !! Là tu pars de la fin, et tu ne prouves rien du tout ! =) en fait, je t'avais montré comment faire dans mon dernier message mais tu ne l'as sans doute pas vu ! ^^

[thomas-buz]

non non non !! Là tu pars de la fin, et tu ne prouves rien du tout ! =) en fait, je t'avais montré comment faire dans mon dernier message mais tu ne l'as sans doute pas vu ! ^^

Ah oui exact autant pour moi
Alors en faite d'après l'hypothèse de récurence
(k+1)!= (k+1)k!>= 2^k-1(k+1)

ou la avec (k+1)k: >= (k+1)2^k/2 >= 2^k ma démnstration est finit ?

[globule rouge]

Ah oui exact autant pour moi
Alors en faite d'après l'hypothèse de récurence
(k+1)!= (k+1)k!>= 2^k-1(k+1)

ou la avec (k+1)k: >= (k+1)2^k/2 >= 2^k ma démnstration est finit ?

oui =) en justifiant que

[thomas-buz]

oui =) en justifiant que

k+1>=2 d'ou (k+1)/2 >= 1
d'ou 2^k * (k+1)/2 >= 2^k

Mais en faite j'ai l'impression de tourner en rond :s

[globule rouge]

k+1>=2 d'ou (k+1)/2 >= 1
d'ou 2^k * (k+1)/2 >= 2^k

Mais en faite j'ai l'impression de tourner en rond :s

bah non pas du tout car quand tu as montré que , tu as fini puisqu'on sait que ! =)

Julie

[thomas-buz]

bah non pas du tout car quand tu as montré que , tu as fini puisqu'on sait que ! =)

Julie

Ah oui d'accord merci beaucoup

[thomas-buz]

bah non pas du tout car quand tu as montré que , tu as fini puisqu'on sait que ! =)

Julie

J'aurai encore une question XD

Si je veux par exemple prouver que
Un=Somme (k=1 de n) 1/k! est majorée il faudrait que je m'y prenne comment ?

[globule rouge]

J'aurai encore une question XD

Si je veux par exemple prouver que
Un=Somme (k=1 de n) 1/k! est majorée il faudrait que je m'y prenne comment ?

il faudrait d'abord partir de la définition de suite majorée !
Une suite est majorée .
Il me semble qu'il faudrait montrer que converge.

[thomas-buz]

il faudrait d'abord partir de la définition de suite majorée !
Une suite est majorée .
Il me semble qu'il faudrait montrer que converge.

et il faudrait procédé comment ?

[globule rouge]

et il faudrait procédé comment ?

Je sais pas vraiment ^^
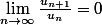
Mais je montrerais que puisqu'il semble logique qu'une série converge en l'infini si le rapport de deux termes successifs tend vers 0...
Ce qui est ici vrai car
Cela reste tout de même à confirmer !!

Julie

[Euler07]

Je sais pas vraiment ^^
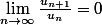
Mais je montrerais que puisqu'il semble logique qu'une série converge en l'infini si le rapport de deux termes successifs tend vers 0...
Ce qui est ici vrai car
Cela reste tout de même à confirmer !!

Julie

Ce servir de la première question en prenant l'inverse

:livre:

[globule rouge]

Ce servir de la première question en prenant l'inverse

:livre:

ah oui je suis bête ^^ merci Euler !

[thomas-buz]

Ce servir de la première question en prenant l'inverse

:livre:

Et si j'ai prouver qu'elle convergé celà ne prouve pas que la suite est majorée ?