Aide devoir etude de fonctions

par **Kameron** » 11 Juin 2006, 09:08

Ah mais oui! je viens de comprendre!
Je vais m'empresser de tracer les courbes et d'attaquer la partie B :)

par **Nicolas_75** » 11 Juin 2006, 09:10

Très bien !
Je t'ai détaillé une réponse possible pour a < 0 deux messages ci-dessus.

par **Kameron** » 11 Juin 2006, 09:15

Ah! merci :)

Par contre, pour tracer les courbes ,quelles valeurs de a devrais-je prendre? (j'ai pris a=1 pour C1 et C-1)

par **Nicolas_75** » 11 Juin 2006, 09:17

L'énoncé me semble clair.
Tu prends a=1 et tu traces

et la courbe représentative de

Tu prends a=-1 et tu traces

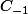
et la courbe représentative de

par **Kameron** » 11 Juin 2006, 09:26

Ah oui je n'avais pas fait attention :/

J'ai tracé les courbes, je suis en train de chercher la 1a de la PARTIE B.

par **Kameron** » 11 Juin 2006, 09:32

Je crains être bloqué :/ faut-il dissocier la fonction en un produit de deux fonctions élevées au carré? :x

par **Nicolas_75** » 11 Juin 2006, 09:36

B.1.a
Pour montrer que

vérifie (1), il suffit de montrer que, pour tout x et y :

Il suffit de remplacer !

EDIT : remplacer tous les

par des

par **Nicolas_75** » 11 Juin 2006, 09:37

Puis, pour B.1.b, prends x=y=0 et déduis-en une équation produit que g(0) doit satisfaire, puis conclus.

par **Kameron** » 11 Juin 2006, 09:55

J'écris plein de trucs sur mon brouillon depuis un moment, mais menant tous à la même finalité: rien ... :mur:

par **Nicolas_75** » 11 Juin 2006, 09:56

Pour quelle question ?

par **Kameron** » 11 Juin 2006, 09:58

Si je fais correctement ce que tu dis, je trouve ga(x).ga(y)=racine²(1)

EDIT:

Pour la question 1b

par **Nicolas_75** » 11 Juin 2006, 09:59

Je répète. Tu es en train de traiter quelle question ?

par **Nicolas_75** » 11 Juin 2006, 10:05

Je ne comprends pas ce que tu fais.
Dans la question B.1.b :
- il n'y a plus de ga : on s'intéresse à une fonction g quelconque vérifiant (1)
- il n'y a plus de x et y puisque je t'ai dit de prendre x=y=0
Il ne doit plus rester qu'une équation avec g(0) !

par **Kameron** » 11 Juin 2006, 10:10

Franchement la je vois pas... je suis un peu perdu

par **Nicolas_75** » 11 Juin 2006, 10:12

B.1.b.
Soit

une fonction vérifiant (1).
On prend

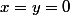
dans (1). On obtient :

On applique deux fois (EDIT : trois fois) une identité remarquable connue :

Donc g(0) ne peut être égal qu'à 0, 1 ou -1

par **Kameron** » 11 Juin 2006, 10:17

Arf! J'avais trouvé g(0)²=g(0)^4 , mais après faut y penser aux identités remarquables :/ Je manque d'entrainement surement :/

par **Nicolas_75** » 11 Juin 2006, 10:25

Je dois m'absenter. Bon courage pour la suite.

par **Kameron** » 11 Juin 2006, 10:28

Merci beaucoup pour ton aide en tout cas elle m'a été très précieuse :)
Si tu lis ceci avant de partir pourrait tu me dire ce qu'est une application nulle? :x

Merci encore. Si quelqu'un peut m'aider pour la suite, je ne pourrais qu'être ravis :)

par **Nicolas_75** » 11 Juin 2006, 10:29

Remarque : tu avais au moins 2 autres méthodes !

Prendre la racine carrée :

c'est-à-dire :

puis équation du 2nd degré ou factorisation

ou

Poser

par **Nicolas_75** » 11 Juin 2006, 10:29

Je t'en prie. :)

Une application nulle est une application constante égale à 0 : pour tout x, f(x)=0

Aide devoir etude de fonctions

Qui est en ligne