Equation différentielle linéaires...

[sousou21000]

Bonjour a tous je bloque pour mon problème si vous pouvez me débloquer un petit peu svp :)

2xy'+y=1/(x+1)

1 ère étape : je l'ai mis sous la forme y'+a(x).y=b(x)
et j'ai considérer que b(x)=0 pour trouver y sans second membre.

Sa donne : y'+y/2x=0
dy/dx=-y/2x
dy/y=-dx/2x
Ensuite on intègre
ln(y)=-1/2ln(x)+K K étant une constante
y=exp(-1/2ln(x)+K)
et c'est la que je bloque en fait je sais pas trop quoi faire du 1/2

Est ce que j'ai le droit de dire que y=-1/2.x.exp(K) ?

Merci de m'aider sa serait sympa !

[Elerinna]

Saurais-tu déjà que : ? Simplifier ensuite devient aisé.

[sousou21000]

Merci pour ta reponse :)
Alors si jai bien compris :
y=x^(-1/2) sans la constante ?

et jai pas le droit de dire que la primitive de 1/(2x) est ln(2x) ?

[Elerinna]

La primitive est identifiée à la constante K près. Cependant, si la condition initiale est connue, K aussi.
Attention au coefficient multiplicatif à la trappe car une primitive de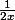 sera :

[sousou21000]

ah oui c vrai autant pour moi !
Bin Merci beaucoup donc j'avance j'en suis à la :
y (sans second membre)=µx^(-1/2) avec µ= exp(K)

2 éme étape : trouver une solution particulière de y
d[µx^(-1/2)]/dx + [µx^(-1/2)] / 2x = 1/(2x^2+2)

J'ai dérivé µx^(-1/2) jai trouver : µ'.x^(-1/2) - µ.[1/2.x^(3/2)]

Après sa me fait :
µ'.x^(-1/2) - µ.[1/2.x^(3/2)] + [µx^(-1/2)] / 2x = 1/(2x^2+2)

Mais la c'est bizard que j'arrive rien a simplifier ?

[sousou21000]

ok je crois que je me suis tromper en dérivant µx^(-1/2) j'ai trouver :
c'est de la forme u'v+v'u
µ'.x^(-1/2) - µ.[µx^(-1/2)] / 2x car x^(-1/2) est de la forme 1/u
Donc en fait sa se simplifie si je n'est pas fait d'erreur !

[sousou21000]

Maintenant il me reste plus qu'a trouver la primitive de (;)x)/(2x^2+2x)
...