Discrimination d'un nombre premier
Olympiades mathématiques, énigmes et défis
-
elmardi
- Messages: 3
- Enregistré le: 04 Jan 2012, 04:04
-
 par elmardi » 04 Jan 2012, 04:16
par elmardi » 04 Jan 2012, 04:16
Bonjour,
Bien que n'ayant qu'un BAC+2 en informatique, je pense avoir trouvé une formule pour discriminer les nombres premiers, et je désirerais donc la mettre à l'épreuve. Et si jamais elle résiste, peut-on la simplifier ?
La voici en langage informatique :
Soit n un nombre entier impair ou premier supérieur ou égal à 5,
Si ((2^(n-1)) - 1)/n donne un résultat Entier, alors, n est premier.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 04 Jan 2012, 09:15
par SaintAmand » 04 Jan 2012, 09:15
Bonjour,
elmardi a écrit:Soit n un nombre entier impair ou premier supérieur ou égal à 5,
Si ((2^(n-1)) - 1)/n donne un résultat Entier, alors, n est premier.
L'hypothèse «n nombre premier» est inutile (un nombre premier supérieur à 2 est nécessairement impair).
Ta conjecture est fausse: 341 divise

et pourtant 341 = 11x31. En revanche, la réciproque:
Si p est un nombre premier>2, alors p divise
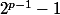
est vraie. C'est un cas particulier du petit théorème de Fermat:
Si p est un nombre premier, et si a est un entier non divisible par p, alors p divise
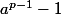
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Jan 2012, 17:22
par leon1789 » 11 Jan 2012, 17:22
elmardi a écrit:Bonjour,
Bien que n'ayant qu'un BAC+2 en informatique, je pense avoir trouvé une formule pour discriminer les nombres premiers, et je désirerais donc la mettre à l'épreuve. Et si jamais elle résiste, peut-on la simplifier ?
La voici en langage informatique :
L'implication est fausse pour n=341.
voir "nombres pseudo-premiers" de base 2 :
http://fr.wikipedia.org/wiki/Nombre_pseudopremier
-
Amberss
- Membre Naturel
- Messages: 22
- Enregistré le: 05 Mar 2012, 08:45
-
 par Amberss » 05 Mar 2012, 14:02
par Amberss » 05 Mar 2012, 14:02
est vraie. C'est un cas particulier du petit théorème de Fermat:

-
Elerinna
- Membre Rationnel
- Messages: 559
- Enregistré le: 27 Fév 2012, 18:59
-
 par Elerinna » 05 Mar 2012, 17:27
par Elerinna » 05 Mar 2012, 17:27
Le libellé exact est : Si p est un entier premier alors

,
)
ou (petit théorème):

-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 05 Mar 2012, 19:03
par nodjim » 05 Mar 2012, 19:03
Il n'empêche, c'est bien par cette méthode que les grands nombres probablement premiers sont cherchés pour servir dans le codage RSA. On les dit probablement premiers car il y a peu de nombres composés qui ont cette propriété.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités

