Application Linéaire.

[Chakir]

Bonsoir ! un peu d'aide SVP.



Considérons l'espace vectoriel R[X] de tous les polynomes en X à coefficient réels, de degré inférieur ou égal à n. On se propose de montrer que le sous-ensemble :
F = { p ;) R[X] tel que P(1)=0 }

est un sous-espace de R[X] de dimension n.

1) De quelle application linéaire F est-il noyeau ? Conclure
2) Vérifier que cette application est surjective.
3) En déduire que Dim F = n.

[Dinozzo13]

Salut !

Qu'as-tu commencer à faire ?
Connais-tu la définition du noyau d'une application linéaire ?

[Chakir]

bonsoir,

ce que je sais c'est que le noyeau d'une application linéaire est donner par :
Ker f = { x;)R tq f(x)=0}

voila avec quoi j'ai commencer :

F = { p ;) R[X] tel que P(1)=0 }
=> Ker f = { p ;) R[X] tel que P(1)=0 } mais dés là je ne sais plus quoi faire ! :mur:

[alm]

Salut,

@chakir:
Si tu exploites bien la question qui t'est posée par Dinozzo13, tu pourras arriver à résoudre ton problème.
Il te pose une question précise : Quel est le noyau d'une application linéaire ?
Tu as répondu :

bonsoir,

ce que je sais c'est que le noyeau d'une application linéaire est donner par :
Ker f = { x;)R tq f(x)=0}

Réponse insuffisante et sans sens car :

• Tu as parlé de sans la présenter
• Qui dit application linéaire dit une application qui a un ensemble de départ et un ensemble d'arrivé (qui en l'occurence sont des espaces vestoriels.
• On voit que pour toi est toujours une partie de , chose non correcte.

Si tu a jetté un coup d'oeil sur ton cours cela auarit pu t'aider .

Tout à coup, on voit que tu dis :

=> Ker f = { p R[X] tel que P(1)=0 } ...

Donc cette fois ci 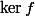devient une partie de 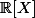, ce qui contredit ta première définition.

Tu es donc invité à :
construire une application linéaire , pour laquelle tu préciseras avec soin :
- L'ensemble de départ (qui doit être un espace vectoriel réel)
- L'nesemble d'arrivé (idem)
- L'image d'un élément de l'ensemble de départ.
verifier qu'elle est effectivement linéaire
[/tex]\bullet[/tex] Veiller au cours de cette construction d'examiner l'énoncé de ton exercice car c'est ça qui va t'aider à tout faire : tu as déjà fait un pas car tu avais traduit : en . Autrement dit tu as presque découvert que : . Alors : comme tu sais l'ensemble parcouru par , tu as déjà l'nsemble de départ ... et comme tu sais que l'image de est un nombre réel tu as aussi l'arrivé . Finalement tu as de façon claire l'image de par ....
Le reste est facile car ton cours dit que : Le noyau d'une application linéaire est un sous-espace vectoriel de l'espace de départ .. comme il dit quelque chose sur l'image d'une application linéaire que je te laisse rappeler toi même.
Si tu examines comme espace vectoriel :
- quels sont ses sous-espaces vectoriels ?
- L'iamge de est donc lequel d'entre ces sous-espaces vectoriels ?
- Le théorème du rang: ça te dit quelque chose ?