Nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 18:22
par samgave » 12 Fév 2012, 18:22
bonjour,
j'ai un exo et je crois que je bloque;
voici l'énoncé:
On désigne par
i le nombre complexe de module 1 et d'argument

;
m étant un parametre réel, on considère le nombre complexe
Zm défini par:

Calculer la partie réelle et la partie imaginaire de Zm;
j'ai multiplié le dénominateur par le conjugué soit:
+i\frac{\sqrt3}{2}]}\times{[(\frac{-1}{2}-m)-i\frac{\sqrt3}{2}]})
car j'ai considéré
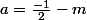
et
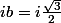
puis le numérateur:
+i\frac{\sqrt3}{2}]}\times{[(\frac{-1}{2}-m)-i\frac{\sqrt3}{2}]})
et en finalité j'arrive à
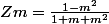
pour continuer il faut que définisse les valeurs de m car apparement le nombre complexe est un réel pur ?
quelque chose m'échappe?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Fév 2012, 19:38
par raito123 » 12 Fév 2012, 19:38
Bonsoir,
Tu t'es trompé dans le calcul du numérateur, le nombre Z_m n'est pas réel pur : par exemple pour m = 1/2!!
Les multiples ne doivent pas être utilisés sans nécessité
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 20:48
par samgave » 12 Fév 2012, 20:48
raito123 a écrit:Bonsoir,
Tu t'es trompé dans le calcul du numérateur, le nombre Z_m n'est pas réel pur : par exemple pour m = 1/2!!
merci pour la verif
je trouve pour le numérateur

ok?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Fév 2012, 20:54
par raito123 » 12 Fév 2012, 20:54
C'est bon :D :)
Les multiples ne doivent pas être utilisés sans nécessité
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 21:55
par samgave » 12 Fév 2012, 21:55
raito123 a écrit:C'est bon


donc maintenant j'ai
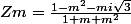
donc la partie imaginaire, c'est le réel

?
et pour déterminer la partie réelle du complexe je fais comment avec le parametre m ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Fév 2012, 22:11
par raito123 » 12 Fév 2012, 22:11
Non ... soit un nombre complexe z = a+ib ou a et b sont des réels ... la partie réelle de z est a et la partie imaginaire est b ...
Dans ton exercice la partie réelle est (1-m²)/(1+m+m²) et la partie imaginaire c'est -m*(racinede 3 )/(1+m+m²)
Les multiples ne doivent pas être utilisés sans nécessité
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 22:23
par samgave » 12 Fév 2012, 22:23
raito123 a écrit:Non ... soit un nombre complexe z = a+ib ou a et b sont des réels ... la partie réelle de z est a et la partie imaginaire est b ...
Dans ton exercice la partie réelle est (1-m²)/(1+m+m²) et la partie imaginaire c'est -m*(racinede 3 )/(1+m+m²)
m'en doutais; donc faut que je determine le quotient pour trouver la partie reelle?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Fév 2012, 22:39
par raito123 » 12 Fév 2012, 22:39
Non non tu laisses tout comme ça :)
Les multiples ne doivent pas être utilisés sans nécessité
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 22:46
par samgave » 12 Fév 2012, 22:46
raito123 a écrit:Non non tu laisses tout comme ça

excuse moi croyait t'avoir donné la suite de l'exo qui dit:
Déterminer les valeurs de
m pour lesquelles la partie réelle de
Zm est nulle.
Calculer le module et un argument de Zm pour chacune des valeurs de
m obtenues
donc faut bien que je résolve le quotient pour déterminer
m ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Fév 2012, 22:51
par raito123 » 12 Fév 2012, 22:51
hein ... bun tu fais la partie réelle égale à 0 et tu résous léquation en m
Les multiples ne doivent pas être utilisés sans nécessité
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 23:14
par samgave » 12 Fév 2012, 23:14
raito123 a écrit:hein ... bun tu fais la partie réelle égale à 0 et tu résous léquation en m
m=1 ou m=-1
pour calculer le module de
Zm je fais comment avec le parametre m ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Fév 2012, 23:16
par raito123 » 12 Fév 2012, 23:16
samgave a écrit:m=1 ou m=-1
pour calculer le module de Zm je fais comment avec le parametre m ?
tantôt tu remplaces m par 1 et tu calcules le modules tantôt par -1 :we:
Les multiples ne doivent pas être utilisés sans nécessité
-
samgave
- Membre Naturel
- Messages: 61
- Enregistré le: 05 Nov 2011, 19:23
-
 par samgave » 12 Fév 2012, 23:31
par samgave » 12 Fév 2012, 23:31
raito123 a écrit:tantôt tu remplaces m par 1 et tu calcules le modules tantôt par -1 :we:
pk j'cherche les complications?
vais me coucher a demain si t'est dispo car j ai une suite pas mal!! merci et a+ :dodo: :dodo:
-
molro
- Messages: 6
- Enregistré le: 26 Jan 2016, 20:06
-
 par molro » 27 Jan 2016, 19:48
par molro » 27 Jan 2016, 19:48
Bonjour,
Comment faite vous pour arriver a ce résultat pourriez vous décortiquer. J'ai un devoir similaire mais je n'arrive pas a votre résultat,a vrai dire le m me perturbée. Merci de votre aide.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Jan 2016, 18:51
par zygomatique » 28 Jan 2016, 18:51
salut
(1 + 2m + i \sqrt3)}{(1 + 2m)^2 + 3} = ...)
je te laisse calculer intelligemment le numérateur ....

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
molro
- Messages: 6
- Enregistré le: 26 Jan 2016, 20:06
-
 par molro » 25 Fév 2016, 13:31
par molro » 25 Fév 2016, 13:31
(1-4m2-4mi√3+3)/(1+4m+4m2+3)=1-m2-im√3)/1+m2+m.
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 104 invités
