Densité

[izoard]

Bonjour,
je dispose de muni de la norme infinie
J'aimerai montrer que est dense dans X .

Je suis parti d'une fonction u dans X et je n'ai pas réussi à fabriquer une suite dans Y tq

Merci d'avance

[Doraki]

Est-ce que tu connais un autre ensemble bien connu qui est dense dans X ?

[izoard]

L'ensemble est dense dans
Par consequent
Or
Donc si on prend l'adherence dans X de cette chaine d'inclusion :

C'est correct ?

[Doraki]

L'ensemble est dense dans
Par consequent
Or
Donc si on prend l'adherence dans X de cette chaine d'inclusion :

C'est correct ?

Euh c'est quoi ton C^0_infini ?
S'il est vraiment inclus dans Y ouais ça marche.

Je pensais aux fonctions polynomiales, ça simplifie un peu le problème mais cet ensemble n'est pas inclus dans Y donc il reste du travail à faire.

[izoard]

J'ai fait un mix de tout ce à quoi je pensais ... :doh:
Je voulais dire les fonctions continues à support compact plutôt notées
Je corrige ça dans le message précédent .
Tu penses que c'est correct ??

[Doraki]

Ben ça ne va pas parcequ'il existe des fonctions continues à support compact qui ne sont pas dérivables en 0, et d'autres qui le sont mais dont la dérivée en 0 n'est pas nulle.
Donc il n'est pas inclus dans Y.

Il faut donc montrer que l'adhérence de Y contient ton ensemble, c'est-à-dire montrer que toutes les fonctions continues à support compact qui ne sont pas dérivables en 0 ou qui le sont mais dont la dérivée en 0 n'est pas nulle peuvent être approchées aussi bien que tu veux par des fonctions de Y.

[izoard]

Exact . Peut être que l'on peut considérer les polynomes de Bernstein

[Doraki]

Exact . Peut être que l'on peut considérer les polynomes de Bernstein

Donc tu remplaces "fonctions continues à support compact nulles en 0" par "fonctions polynomiales nulles en 0" ?
(d'ailleurs comme [0;1] est compact, il n'y a aucune différence entre les fonctions continues et les fonctions continues à support compact, donc c'était idiot)

Il faut donc que tu montres que tout polynôme nul en 0 est approchable par des fonctions de Y (pas forcément par des polynômes)
L'avantage par rapport aux fonctions continues c'est que là ben les fonctions polynomiales sont dérivables, donc ça aide vu qu'on doit approximer par des fonctions dérivables.

Si je prends f(x) = x sur [0;1],
tu ferais quoi comme approximations de f par des fonctions de Y ?

[izoard]

Je recapitule :
Je considère une fonction
J'aimerais trouver une suite de Y qui converge uniformement vers f

Pour cela, j'ai l'idée d'utiliser les polynomes de Bernstein associés à f :


Je sais que cette suite converge uniformement vers f

Si était dans Y, on aurait gagné

On a bien
De plus on a aussi que

CEPENDANT on a

[izoard]

Je recapitule :
Je considère une fonction
J'aimerais trouver une suite de Y qui converge uniformement vers f

Pour cela, j'ai l'idée d'utiliser les polynomes de Bernstein associés à f :


Je sais que cette suite converge uniformement vers f

Si était dans Y, on aurait gagné

On a bien
De plus on a aussi que
CEPENDANT on a
Donc n'est pas dans Y

je cherche donc à modifier les polynomes de Bernstein pour les rendre dans Y sans perdre la convergenge uniforme vers f

Et la je sèche !!!
a le bon gout de tendre vers 0,
mais que dire du n qu'il y a devant ??

[Doraki]

J'ai mis partout 0 à la place de 1 ?

ça me paraît pas une bonne idée ton truc de modifier une construction délicate pour obtenir une suite de fonctions de Y qui tende encore vers f. Je crois pas que ce soit très simple de montrer que les polynomes de bernsein convergent uniformément vers f, alors si en plus tu veux rajouter des trucs dedans ...

comme je le dis depuis le début, je te conseille de chercher à approximer les polynômes qui valent 0 en 1 par des fonctions de Y.
C'est strictement plus facile que de vouloir approximer les fonctions de X parce que là tu te donnes plein d'hypothèses en plus en n'approximant que les polynômes nuls en 1.
Et en conclusion, comme les polynômes nuls en 1 sont denses dans X, bah si tu montres que l'adhérence de Y contient les polynômes nuls en 1, ça montre qu'elle contient aussi X.


Le plus dur c'est de fabriquer des approximations de la fonction g(x) = (x-1).

Peux-tu fabriquer une fonction f dans Y telle que |f(x)-(x-1)| < 1/10 sur [0;1] ?

[izoard]

Une fonction dans Y est nulle en 1 et a une tangente horizontale en ce point .
Je considère la suite et
Mais elle n'est que continue .
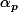
A n fixée, si je la convole par une suite régularisante j'obtiens alors une fonction
qui converge uniformement vers quand p tend vers l'infinie .
Et converge elle même uniformement vers 1-x quand n tend vers l'infini