Je viens demander de l'aide pour une question concernant l'exponentielle.
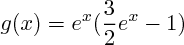
Je dois étudier le signe de g(x) sur ]- infini ; 1]
Donc ce que j'ai fait c'est que j'ai essayé de dériver g(x) mais le e^x me bloque !
J'ai fait de la forme u * v :
u(x) = e^x ; u'(x) = e^x
v(x) = (3/2) e^x -1 ; v'(x) = (3/2) e^x
Donc : u * v = u'v+uv' = e^x (3/2 e^x -1) + e^x(3/2 e^x)
Mais e^x * e^x ça fait combien ??
Je dois dériver cette fonction, faire le tableau de variation de g' ce qui nous permet d'avoir le signe de g(x), c'est ça ?
Merci d'avance de votre aide!
