Aidez-moi à résoudre ce problème!!
Olympiades mathématiques, énigmes et défis
-
mathiasULG
- Messages: 4
- Enregistré le: 02 Juin 2006, 10:08
-
 par mathiasULG » 02 Juin 2006, 10:17
par mathiasULG » 02 Juin 2006, 10:17
bonjour a tous , voilà,
Le truc, c'est qu'on doit ajouter 7 nombres entiers IMPAIRS et le résultat doit donner 40.
bonne chance à tous
ps: la solution existe
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 02 Juin 2006, 10:20
par Zebulon » 02 Juin 2006, 10:20
Bonjour,
vous êtes sûr que c'est 40? La somme de sept entiers impairs est un entier impair.
-
Patastronch
- Membre Irrationnel
- Messages: 1345
- Enregistré le: 22 Aoû 2005, 23:53
-
 par Patastronch » 02 Juin 2006, 10:21
par Patastronch » 02 Juin 2006, 10:21
ajouter un nombre impair de nombre impair donne un nombre impair.
Or 40 est pair, et 7 est impair.
[edit] devancé par Zebulon :)
-
mathiasULG
- Messages: 4
- Enregistré le: 02 Juin 2006, 10:08
-
 par mathiasULG » 02 Juin 2006, 10:35
par mathiasULG » 02 Juin 2006, 10:35
non, mon prof m'assure que la réponse existe. j'espère que qq1 trouvera.
merci
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 02 Juin 2006, 10:39
par Zebulon » 02 Juin 2006, 10:39
La preuve est simple :
soient sept entiers impairs, ils s'écrivent

,

,...,

. On les additionne, ce qui donne :
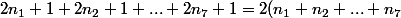+7=2(n_1+n_2+...+n_7+3)+1)
donc ce nombre est impair!
-
mathiasULG
- Messages: 4
- Enregistré le: 02 Juin 2006, 10:08
-
 par mathiasULG » 02 Juin 2006, 10:42
par mathiasULG » 02 Juin 2006, 10:42
c'est ce que j'ai dit à mon prof mais il dit que la solution existe et que son fils de 13 ans l'a trouvé, alors tu vois ds quelle situation je suis. si tu connais qq1 susceptible de trouver please aide moi :mur:
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 02 Juin 2006, 11:04
par BancH » 02 Juin 2006, 11:04
mathiasULG a écrit:Le truc, c'est qu'on doit ajouter 7 nombres entiers IMPAIRS et le résultat doit donner 40.
Soit il a une de ces quatre données fausse, soit ton prof te fait marcher

-
mathiasULG
- Messages: 4
- Enregistré le: 02 Juin 2006, 10:08
-
 par mathiasULG » 02 Juin 2006, 11:06
par mathiasULG » 02 Juin 2006, 11:06
il ne peut pas me faire marcher il a donné ce problème devant tout les profs et la proviseur.
merci quant même. :++:
-
scelerat
- Membre Relatif
- Messages: 397
- Enregistré le: 03 Aoû 2005, 13:37
-
 par scelerat » 02 Juin 2006, 13:13
par scelerat » 02 Juin 2006, 13:13
Le prof a-t-il dit positifs ?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 02 Juin 2006, 13:17
par BancH » 02 Juin 2006, 13:17
La somme d'un nombre impair d'entiers relatifs impairs est impaire.
-
toup
- Messages: 5
- Enregistré le: 02 Juin 2006, 15:26
-
 par toup » 02 Juin 2006, 15:56
par toup » 02 Juin 2006, 15:56
0 n'est ni impaire ni paire je croit il donc possible de l'utilisé non?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 02 Juin 2006, 16:01
par BancH » 02 Juin 2006, 16:01
Non, zéro est bien pair.
Et puis si comme tu dis zéro n'étais ni impair ni pair alors il ne peut pas être utilisé car les nombres utilisés sont tous impairs.
Mais y a pas à se creuser la tête.... il n'y a pas de solution !!!
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 04 Juin 2006, 13:25
par theluckyluke » 04 Juin 2006, 13:25
mathiasULG a écrit:c'est ce que j'ai dit à mon prof mais il dit que la solution existe et que son fils de 13 ans l'a trouvé, alors tu vois ds quelle situation je suis. si tu connais qq1 susceptible de trouver please aide moi :mur:
t'es sûr qu'il a un fils? je suis pour l'avis qu'il te fais marcher...
-
murray
- Membre Naturel
- Messages: 84
- Enregistré le: 17 Mai 2006, 17:50
-
 par murray » 04 Juin 2006, 16:37
par murray » 04 Juin 2006, 16:37
A mon avis, la seule solution serait de ne pas raisonner en base 10.
La parité semble en effet dépendre de la base choisie:
Par exemple A= 7^3+ 7^2+7^1 +1 s'ecrit 1111 en base 7 et 400 en base 10
-
murray
- Membre Naturel
- Messages: 84
- Enregistré le: 17 Mai 2006, 17:50
-
 par murray » 04 Juin 2006, 17:21
par murray » 04 Juin 2006, 17:21
suivant l'idée de mon dernier message, 40 s'écrit 13 en base 5.
Et 13=1+3+1+1+3+3+1
Je ne sais pas si c'est la réponse que ton prof de maths attend.
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 04 Juin 2006, 17:24
par Quidam » 04 Juin 2006, 17:24
murray a écrit:40 s'écrit 13 en base 5.
Correction : 40 s'écrit 130 en base 5
... et de toutes manières 1+3+1+1+3+3+1=23 en base 5 !
:arme3:
Quelle que soit la base b, un nombre impair est un nombre impair (qui osera le nier ?), et 40 = 4*b est bel et bien un nombre pair !!!!
:arme3:
-
lolor
- Membre Naturel
- Messages: 64
- Enregistré le: 01 Mai 2005, 01:14
-
 par lolor » 04 Juin 2006, 18:52
par lolor » 04 Juin 2006, 18:52
bonjour, je me joint à votre recherche de solution
En effet, le changement de base ne règle pas notre pb et de toute façon ça m'etonnerai que son gamin de 13 ans ait fait des changements de bases.
ça serait pas une histoire d'écriture des chiffres du genre "13" s'écrit avec 2 chiffres impairs 1 et 3 donc compte pour deux impairs ?
dans ce cas, 7+13+3+3+7+7=40 convient
je trouve cette solution un peu nulle mais si il a voulu vous faire marcher... Enfin bon je crois que l'idée de jouer sur les mots viendrait facilement à l'esprit d'un enfant de 13 ans
-
Tqup3
- Membre Naturel
- Messages: 74
- Enregistré le: 27 Mai 2006, 20:22
-
 par Tqup3 » 04 Juin 2006, 19:00
par Tqup3 » 04 Juin 2006, 19:00
Il me semblait que 0 était à la fois pair et impair: en effet 0=2k*0 pour kZ et 0=(2k+1)*0 pour kZ. Dans ce cas on peut l'utiliser. dites si j'ai dit une grosse bêtise :)
Dans ce cas 40=39+1+0+0+0+0+0
J'avoue c'est encore plus nul que la solution de lolor...
-
murray
- Membre Naturel
- Messages: 84
- Enregistré le: 17 Mai 2006, 17:50
-
 par murray » 04 Juin 2006, 19:17
par murray » 04 Juin 2006, 19:17
Quidam a écrit:
Quelle que soit la base b, un nombre impair est un nombre impair (qui osera le nier ?), et 40 = 4*b est bel et bien un nombre pair !!!!
:arme3:
mea culpa pour ma solution.
ceci dit si je reprends ma proposition 7^3+7^2+7^1+1 est impair en base 7 et pair en base 10. IL en est de même de 40 qui s'écrit 1111 en base 3
Néanmoins, je pense que la notion de parité n'a plus de sens lorsqu'on ne se place plus en base 10
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 04 Juin 2006, 19:32
par theluckyluke » 04 Juin 2006, 19:32
Et si la solution était qu'il n'y a pas de solution? :marteau:
ok... je sors
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
