Fonction linéaire non continue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
patrickjaud
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Sep 2008, 09:39
-
 par patrickjaud » 29 Jan 2012, 20:33
par patrickjaud » 29 Jan 2012, 20:33
bonjour à tous,
je cherche une fonction linéaire non continue
1) il semble que L : R[X]-->R[X] , L(P) = P' n'y soit pas !
ainsi M :R[X]---> R[X], M(P(X)) = X P(X), on a L o M - M o L = Id
2) j'ai montré que
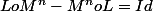
aussi pour tout n entier !
voici ma question sur lequel je bloque j'aimerais obtenir une contradiction sur le fait que M et L sont continues avec le 2) ! je n'y arrive pas
merci d'avance de vos réponses !
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 29 Jan 2012, 20:45
par SaintAmand » 29 Jan 2012, 20:45
Bonsoir,
patrickjaud a écrit:je cherche une fonction linéaire non continue
1) il semble que L : R[X]-->R[X] , L(P) = P' n'y soit pas !
Ça dépend de la topologie choisie pour R[X].
-
patrickjaud
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Sep 2008, 09:39
-
 par patrickjaud » 29 Jan 2012, 21:33
par patrickjaud » 29 Jan 2012, 21:33
SaintAmand a écrit:Bonsoir,
Ça dépend de la topologie choisie pour R[X].
oui en effet, je pense à un espace normé avec la norme suivante
 \mid / x \in [-1; 1] \})
pourrait faire l'affaire.
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 30 Jan 2012, 20:46
par SaintAmand » 30 Jan 2012, 20:46
patrickjaud a écrit:oui en effet, je pense à un espace normé avec la norme suivante
 \mid / x \in [-1; 1] \})
pourrait faire l'affaire.
Soit la forme linéaire
)
. Tu peux trouver une suite
_n)
qui converge vers 0 tel que
)_n)
diverge.
-
patrickjaud
- Membre Naturel
- Messages: 17
- Enregistré le: 08 Sep 2008, 09:39
-
 par patrickjaud » 30 Jan 2012, 21:39
par patrickjaud » 30 Jan 2012, 21:39
SaintAmand a écrit:Soit la forme linéaire
)
. Tu peux trouver une suite
_n)
qui converge vers 0 tel que
)_n)
diverge.
Merci SaintAmand
Ta fonction
)
est bien une forme linéaire !
oui il semble que
 =\frac{x^n}{n})
fonctionne bien pour la norme que j'ai proposé !
 / x \in [-1;1] \} = \frac {1}{n})
et cela tend bien vers 0.
alors que ta fonction
 = \frac{3^n}{n})
tend vers

par contre l'espace R[X} n'est pas complet !
et si on se place dans un espace complet comme les fonctions continues sur [-4,+4] là la norme que j'ai proposé n'est pas une norme pour cette espace ! mince
existe il alors une fonction voire une forme linéaire non continue définie sur un espace de Banach ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
