Chaine en rotation

[killyan]

Bonjour à tous,

Dans le cadre de mon boulot je souhaite tracer le profil que prend une chaine accrochée au sommet et au pied d'un mat vertical. Le mat est mis en rotation et la chaine se déploye.
Je souhaite établir différentes courbes en faisant varier les paramètres suivants:

Hauteur du mat (distance entre les points d'accrochage haut et bas)
Longueur de la chaine
Poids de la chaine
Vitesse de rotation

Application: Le mat est placé dans une cuve cylindrique dont le fond est incliné à 45°.
La chaine mise en rotation ne doit pas venir en contact avec les parois.

Si vous pouviez m'aiguiller pour determiner ces courbes.

En vous remerciant

Killyan

[Mathusalem]

Salut,
Je te garantis pas l'existence d'une solution analytique pour la forme de la courbe, mais pour info : est-ce que le mat est aussi incliné de à 45 degrés par rapport à la verticale s'il est au fond du cylindre ?

[killyan]

Salut,
Je te garantis pas l'existence d'une solution analytique pour la forme de la courbe, mais pour info : est-ce que le mat est aussi incliné de à 45 degrés par rapport à la verticale s'il est au fond du cylindre ?

Le mat est en position verticale. La cuve est constituée d'une partie cylindrique verticale et d'un fond conique .

Merci de t'interresser à mon problème

Killyan

[Mathusalem]

Je crois que tu devrais regarder plutôt experimentalement et déduire certaines relations..

Si tu dis que le mat sur lequel la chaine est accrochee est l'axe x, et y(x) le profil de ta chainette, le profil y(x) répond a l'équation différentielle (si je me suis pas gourré)



Avec la vitesse de rotation, g la gravité, et un paramètre (multiplicateur de lagrange dûe à la contrainte sur la longueur de la chaîne).

J'ai pas essayé de trouver une solution mais je suis pas optimiste. On pourrait regarder la gueule de la fonction en faisant une intégration numérique, mais le problème c'est qu'il faudrait fixer les paramètres du problème alors que toi tu veux une fonction dépendant de ces paramètres qui décrit ta courbe...

[Dlzlogic]

Bonjour,
Je suppose que si la chaîne tourne, c'est pour mélanger quelque-chose.
Supposons que la vitesse de rotation soit suffisante pour que g devienne négligeable. En ce cas, la courbe prise par la chaine est une chainette (celle adoptée par les câbles de transport d'électricité).
Que se passe-t-il entre le moment du départ où tout est immobile et la rotation à vitesse normale ? Un ressort pourrait résoudre ce problème.

Si j'avais à réaliser cela, je prendrais en photo une corde à sauter avec différentes longueurs.
Je numériserais ces courbes, ou plutôt 1/2 courbes. Par exemple on pourra vérifier qu'à partir d'une certaine vitesse la forme ne change pas.
Même expérience avec une chaine à sauter, et comparaison des courbes pour un changement important de la densité de la "corde".
Je pense que vous devriez trouver une fonction de la 1/2 courbe, assez facilement. La répétition d'expérience vous permettra de connaitre la précision du résultat. Suivant le cas, soit l'adopter, soit provoquer d'autres expériences.

[Mathusalem]

Bonjour,

Supposons que la vitesse de rotation soit suffisante pour que g devienne négligeable. En ce cas, la courbe prise par la chaine est une chainette (celle adoptée par les câbles de transport d'électricité).

Le potentiel de la centrifuge dépend de la distance au carré si je ne m'abuse. Le problème d'optimisation sous-contrainte résolu analytiquement (wolfram) fait alors intervenir tout un tas d'objets comme des integrales elliptiques etc... Ça vient de l'équation différentielle suivante :



Remarque dans ce cas il est assez simple de faire un schéma numérique pour construire la gueule de la fonction. Ça devrait donner une courbe plus resserrée qu'un cosh, mais semblable.

Ca ne change pas le fait que ça ne répond pas au problème. Je comprends pas trop ce que tu veux faire Dlzlogic, mais il est clair qu'il faut atteindre une vitesse de rotation considérable pour totalement négliger la gravité.

Puisque le problème est invariant de taille, je conseillerais à Kilyan de faire une maquette modèle réduit et voir comment ça se comporte.

[Dlzlogic]

Ca ne change pas le fait que ça ne répond pas au problème. Je comprends pas trop ce que tu veux faire Dlzlogic, mais il est clair qu'il faut atteindre une vitesse de rotation considérable pour totalement négliger la gravité.

Petite expérience simple : sur la plage, un enfant a un sceau rempli d'eau. il le fait tourner, par dessus sa tête ou comme la grande roue, pas une seule goutte d'eau ne s'échappe. En un demi-tout le sceau a donc atteint une vitesse de rotation suffisamment considérable pour totalement contrer la gravité.

Ma suggestion consiste à dire qu'avant d'entamer des théories compliquées, qu'il faudra de toute façon valider, il serait peut être plus simple de commencer par chercher une relation simple entre la longueur de la chaine et son écartement par rapport à l'axe de rotation.
Il ne faut pas oublier l'usure de la chaine, donc son allongement, qui provoquera une augmentation de l'écartement du même ordre de grandeur.

Si la résolution de l'équation est trop compliquée, une division de la chaine en nombre pair de maillons (une dizaine), donnera une équation approchée, mais probablement beaucoup plus facile à résoudre.

[killyan]

Bonjour à vous deux,

Pour mieux comprendre le système je précise le mode de fonctionnement du système.

Une des extrémités de la chaine est fixée en pied du mat
L'autre extrémité est fixée à un contre-poids logé dans le mat (tube creux).
En tête de mat la chaine passe par une poulie pour descendre dans le mat jusqu'au contre poids.

A l'arrêt:La chaine est contre le mât tendue par l'action du contre-poids.
Le contre-poids est en partie basse du mât.

A la mise en rotation du mat:La force centrifuge déploye la chaine et le contre poids monte dans le mat jusqu'a une butée.

Une image serait plus explicite mais la fonction insérer une image ne fonctionne pas.

Je souhaite représenter le profil que prend la chaine lorsqu'elle est entièrement déployée (contre-poids en butée ) et cela pour plusieurs longueur de chaine et longueur le mat.

Il m'est par contre difficile de réaliser des essais grandeur nature.

L'usure de la chaine n'est pas à prendre en compte (c'est de l'entretien, il suffit de retirer un ou plusieurs maillons pour conserver sa longueur)

La vitesse de rotation ne doit pas être trop élevée mais suffisante pour déployer la chaine.
Dans ce cas le poids de la chaine n'est peut être pas totalement négligeable?

Mais si en négligeant le poids de la chaine il existe une relation simple entre la longueur de la chaine et son écartement par rapport à l'axe de rotation, cette première approximation est peut être suffisante.

[Mathusalem]

La vitesse de rotation ne doit pas être trop élevée mais suffisante pour déployer la chaine.
Dans ce cas le poids de la chaine n'est peut être pas totalement négligeable?

Mais si en négligeant le poids de la chaine il existe une relation simple entre la longueur de la chaine et son écartement par rapport à l'axe de rotation, cette première approximation est peut être suffisante.

Salut, enfait c'est pas important de savoir les infos sur le contrepoids, a moins de vouloir calculer pour quelle vitesse de rotation est-ce que tu vas atteindre la butée, et là je pense que même numériquement c'est long.

Je pense pas que l'on puisse négliger la gravité. L'image du sceau plein d'eau de Dlzlogic n'a rien à voir avec la situation présente. En me plaçant 'dans la chaîne', il y a une 'force centrifuge' dirigée selon un axe perpendiculaire à l'axe de la gravité. En revanche, le rapport de ces forces peut-être tel que l'on néglige la gravité, mais alors à une vitesse de rotation élevée (et ici, on ne sait pas à priori ce que ça veut dire élevé, puisqu'on n'a pas résolu l'équation).

J'essayerai plus tard de poser un schéma pour l'équation différentielle tout en haut que je t'ai donnée, pour voir si on peut en dégager des trucs, mais c'est chaud.

[Skullkid]

Bonjour, j'ai essayé moi aussi de mettre le problème en équation, et j'en suis arrivé à une équa diff beaucoup plus compliquée que celle de Mathusalem (peut-être simplifiable et peut-être tout simplement fausse, j'ai pas encore essayé de la résoudre numériquement) même si elle fait apparaître des termes semblables. Juste une question par rapport à ça : c'est normal que la masse de la chaîne et/ou des valeurs au bord de la tension n'apparaissent nulle part ?

[Mathusalem]

Bonjour, j'ai essayé moi aussi de mettre le problème en équation, et j'en suis arrivé à une équa diff beaucoup plus compliquée que celle de Mathusalem (peut-être simplifiable et peut-être tout simplement fausse, j'ai pas encore essayé de la résoudre numériquement) même si elle fait apparaître des termes semblables. Juste une question par rapport à ça : c'est normal que la masse de la chaîne et/ou des valeurs au bord de la tension n'apparaissent nulle part ?

J'ai mis l'axe x sur le mat (de hauteur H) dirigé vers le haut, et y l'ecart de la chaine par rapport au mat
J'ai posé la fonctionnelle F sous contrainte que int de 0 à H sqrt(1+y'^2)dx = L



J'ai oublié de le recopier, mais ça change que très peu la forme de l'equa diff. J'ai pas considéré les effets de tension de bord. Enfait on peut tout à fait factoriser par rho, et ensuite il se barre dans les equations, ca donne juste un autre sens au multiplicateur de Lagrange.

[Dlzlogic]

Si La lonsueur du mat est grande par rapport à l'écartement maximum, alors, l'écartement maximum est à peu près égal à (C² - L²)/2L
C la longueur de la chaine, L la longueur du mat. (formule à vérifier).
J'appelle écartement la distance maximum entre la chaine et le mat, si on tire au maximum, à partir du milieu.
J'en reviens à mon idée de départ, la photo d'une corde à sauter.
Il est sûr que si on connaissait la longueur du mat et le diamètre de la cuve, on aurait déjà un indication pour cerner les limites du problème.

[Skullkid]

J'ai mis l'axe x sur le mat (de hauteur H) dirigé vers le haut, et y l'ecart de la chaine par rapport au mat
J'ai posé la fonctionnelle F sous contrainte que int de 0 à H sqrt(1+y'^2)dx = L



J'ai oublié de le recopier, mais ça change que très peu la forme de l'equa diff. J'ai pas considéré les effets de tension de bord. Enfait on peut tout à fait factoriser par rho, et ensuite il se barre dans les equations, ca donne juste un autre sens au multiplicateur de Lagrange.

Okédac, j'étais passé par un truc beaucoup moins efficace (les lagrangiens me semblent bien loin malheureusement...) prenant en compte la tension interne de la chaîne...

[killyan]

Salut,

Quelques ordres de grandeur pour mieux visualiser le mécanisme:

Longueur du mat: 6 à 9m
Poids de la chaine: 4 à 5kg/m
Diamètre de la cuve: 5 à 6m
vitesse de rotation: 40 à 60tr/min
Longueur de la chaine: doit s'approcher de la paroi à environ 100mm

[Mathusalem]

Salut,

Quelques ordres de grandeur pour mieux visualiser le mécanisme:

Longueur du mat: 6 à 9m
Poids de la chaine: 4 à 5kg/m
Diamètre de la cuve: 5 à 6m
vitesse de rotation: 40 à 60tr/min
Longueur de la chaine: doit s'approcher de la paroi à environ 100mm

A l'instinct, mais vraiment instinct, je dirais que l'écart maximal depuis le mât ne devrait pas dépasser l'écart maximal du cas où l'on nélige la gravité.
Je m'explique : Dans le cas où l'on néglige la gravité, ta chaînette aura un profil 'parabolique' avec son écart maximum au milieu du mat. L'effet de la gravité est de tirer cette 'bosse' vers le bas et de la réduire.

Un exemple pratique pour se convaincre de cet argument - loin des considérations théoriques, ce qui ne manquera pas de plaire à notre ami Dlzlogic - si tu poses deux doigts sur deux points d'un fil quelconque en laissant un peu de mou, et qu'avec un autre doigt tu écartes le fil vers l'extérieur, tu verras que c'est bien quand t'es au milieu (cas gravité négligée) que l'écart par rapport à "l'axe" est maximal.

Faut juste que je trouve un schéma numérique stable pour plotter



Parce que pour l'instant euler ça diverge bien comme il faut (vu que c'est pas linéaire?..)

Ceci permettrait d'encadrer par le bas la longueur de chaine(i.e tu seras certainement pas dans le cas où la gravité peut être négligée, parce que 40/60 tours minutes c'est pas immense, et donc par rapport à la valeur que je vais essayer de trouver tu pourras rajouter un peu de chaine).

[Dlzlogic]

Bonjour,

loin des considérations théoriques, ce qui ne manquera pas de plaire à notre ami Dlzlogic

C'est gentil de penser à moi pour argumenter.
Je pense à plusieurs choses.
1- étant donné les rapports de longueur et diamètre de cuve, ma formule approchée de l'écartement au mat n'est pas bonne.
2- en supposant que cette chaine sert à malaxer ou mélanger quelque-chose, et la vitesse de rotation faible, j'ai l'impression qu'elle aura du mal à décoller du mat.
3- a supposer qu'elle décolle, mise en rotation, si elle doit effectivement mélanger, la force appliquée à la partie latérale des anneaux sera certainement non négligeable par rapport à la force centrifuge qui maintient sa position. la chaine ne sera donc plus dans un plan vertical et l'écartement s'en trouvera modifié de façon sensible.

[Black Jack]

A l'instinct, mais vraiment instinct, je dirais que l'écart maximal depuis le mât ne devrait pas dépasser l'écart maximal du cas où l'on nélige la gravité.
Je m'explique : Dans le cas où l'on néglige la gravité, ta chaînette aura un profil 'parabolique' avec son écart maximum au milieu du mat. L'effet de la gravité est de tirer cette 'bosse' vers le bas et de la réduire.

Un exemple pratique pour se convaincre de cet argument - loin des considérations théoriques, ce qui ne manquera pas de plaire à notre ami Dlzlogic - si tu poses deux doigts sur deux points d'un fil quelconque en laissant un peu de mou, et qu'avec un autre doigt tu écartes le fil vers l'extérieur, tu verras que c'est bien quand t'es au milieu (cas gravité négligée) que l'écart par rapport à "l'axe" est maximal.

Faut juste que je trouve un schéma numérique stable pour plotter



Parce que pour l'instant euler ça diverge bien comme il faut (vu que c'est pas linéaire?..)

Ceci permettrait d'encadrer par le bas la longueur de chaine(i.e tu seras certainement pas dans le cas où la gravité peut être négligée, parce que 40/60 tours minutes c'est pas immense, et donc par rapport à la valeur que je vais essayer de trouver tu pourras rajouter un peu de chaine).

Sans y avoir longtemps réfléchi (et donc gare aux bêtises), j'ai bien peur que cela divergera toujours avec cette équation.

Si on part, avec un signe+ par exemple, pour y = 0, y' est > 0 et donc y croit et devient > 0.
Mais plus y augmente ... et plus y' est positif et donc emballement.

Même conclusion avec le signe -, emballement vers les y négatifs.

Il me semble que cette équation différentielle impose un y = f(x) avec la "courbure" dans le mauvais sens.

Sauf si je me plante, ce qui est bien possible

:zen:

[Mathusalem]

J'étais arrivé plus ou moins aux même conclusions, je voyais pas comment obtenir un truc qui diverge pas.

Il est possible de séparer les variables et résoudre wolframiquement l'intégrale



Puis l'inverse de ceci serait la courbe que l'on cherche. Mais c'est pas évident à priori, car bien que la primitive soit bijective (donc inversible) ça n'a pas la gueule d'une parabole..C'est comme quand on sépare les variables de le cas de la chaînette, on a le y dans la racine de degré 1, et donc on tombe sur une primitive en arccosh(y) et on conclut alors que y = cosh(x). Mais le truc c'est que l'arccosh(x) quand on l'inverse ça fait qu'une moitié de chaînette... on doit en principe y coller deuxième solution du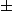 . Mais dans notre cas l'expression à manier est on ne peut plus mystérieuse.



Je vois pas trop à priori comment résoudre le problème. On aurait peut-être plus de chance avec la première équa diff plus moche, mais de ce que je me rappelle dans ce genre d'équa diff non linéaire faut magouiller un bon moment pour la ramener à du linéaire et appliquer des schémas connus..

Bon peut-être me suis aussi gourré dans le calcul, je le referai ce soir p-e.

[killyan]

Bonjour à tous

Je suis impressionné par l'énergie que vous déployez pour résoudre mon problème et que je n'imaginais pas si complexe.
Pour répondre à l'interrogation de Dlzlogic, le système ne sert pas à malaxer ni à mélanger mais à déstructurer un produit qui a tendance à s'agglomérer et à vouter.
Lorsque la cuve est pleine le produit est en contact avec le mat. Lors de l'extraction, la chaine en se déployant vient gratter le produit qui s'émiette et s'évacue par le fond du silo. Il se crée alors un vide, autour du mat, qui prend la forme d'un ballon de rugby. En fin d'extraction la chaine tourne librement dans le cuve mais doit s'approcher suffisamment (50 à 100mm) de la paroi (fond et paroi verticale) pour extraire le produit qui adhère à la cuve mais en aucun cas la heurter au risque de la défoncer.

je cherchais à définir théoriquement s'il y a des configurations où, en fonction du diamètre de la cuve et de sa hauteur (hauteur du mat) il y a un risque de heurter le fond de la cuve.

[killyan]

Bonjour à tous,

S'il n'existe pas de solution simple pour représenter la fonction, y a t-il une méthode permettant de calculer point par point le profil de la courbe. L'utilisation d'un tableur avec si nécessaire des macros est elle envisageable.

Si quequ'un à une idée, elle sera la bienvenue

En vous remerciant