Bonjour,
Pourriez-vous m'aider pour ce devoir de géométrie analytique?
Travail dans le plan muni d'une base orthonormée (o,i,j).
Soient les points A(-4,-4),B(4,1),C(0,3)
Voici les questions:
1)Etablissez les équations - des droites AB,AC,BC
-des médianes du triangle ABC
-des hauteurs du triangle ABC
-des médiatrices du triangle ABC
2)Calculez les coordonnées de l'orthocentre H,du centre du cercle circonscrit M et du centre de gravité G du triangle. Montrez que ces 3 points sont colinéaires.
3)Etablissez l'équation du cercle circonscrit au triangle ABC. Ensuite calculez les coordonnées des points d'intersection de ce cercle avec les axes.
Vous n'êtes pas obligé de me donner les réponses mais j'aimerais être aidé et éclairé parce que je ne vois vraiment pas comment il faut faire.
Est-ce les équations vectorielles ou cartésiennes que je dois faire?
Et pour la 2e question est-ce que je dois calculer avec les vecteurs,etc?
MERCI BEAUCOUP A CEUX QUI POURRONT M'AIDER
Devoir urgent
13 messages
- Page 1 sur 1
slt
pour la première partie, par définition une équation réduite de droite est de la forme y=mx+p, connaissant les coordonnées de 2 points appartenant à cette droite, tu peux identifier m(coeff directeur) et p(ordonnée à l'origine) !
pour les médianes pars de la définition : une médiane ds un triangle est issue d'un sommet et joint le milieu du côté opposé, tu sais calculer les coordonnées du milieu d'un seglent connaissant ses extrémités, et sachant les coordonnées du sommet en question, tu peux aussi identifier m et p ! idem pour les hauteurs, sauf que ds ce cas, tu utilises le vecteur directeur n(a;b) du côté opposé au sommet dont elle est issue est aussi un vecteur normal à cette hauteur, cad qu'elle admet une équation cartésienne de la forme ax+by+c=0 où c est réel, et avec n(a;b) ! rappel, cette droite admet le vecteur g(-b;a) pour vecteur directeur !
pour la première partie, par définition une équation réduite de droite est de la forme y=mx+p, connaissant les coordonnées de 2 points appartenant à cette droite, tu peux identifier m(coeff directeur) et p(ordonnée à l'origine) !
pour les médianes pars de la définition : une médiane ds un triangle est issue d'un sommet et joint le milieu du côté opposé, tu sais calculer les coordonnées du milieu d'un seglent connaissant ses extrémités, et sachant les coordonnées du sommet en question, tu peux aussi identifier m et p ! idem pour les hauteurs, sauf que ds ce cas, tu utilises le vecteur directeur n(a;b) du côté opposé au sommet dont elle est issue est aussi un vecteur normal à cette hauteur, cad qu'elle admet une équation cartésienne de la forme ax+by+c=0 où c est réel, et avec n(a;b) ! rappel, cette droite admet le vecteur g(-b;a) pour vecteur directeur !
reslt
la seconde est assez rapide ! un exemple : pour trouver H l'orthocentre qui est par définition l'intersection des 3 hauteurs du triangle, cannaissant les équations d'o moin 2 de ces hauteurs, par exemple y=mx+p et y1=ax+b, tu cherches leur intersection en résolvant y=y1 ! idem avec le centre de gravité qui est le point de concour des médianes et le centre du cercle circonscrit o triangle qui est l'intersection des 3 médiatrices !
la seconde est assez rapide ! un exemple : pour trouver H l'orthocentre qui est par définition l'intersection des 3 hauteurs du triangle, cannaissant les équations d'o moin 2 de ces hauteurs, par exemple y=mx+p et y1=ax+b, tu cherches leur intersection en résolvant y=y1 ! idem avec le centre de gravité qui est le point de concour des médianes et le centre du cercle circonscrit o triangle qui est l'intersection des 3 médiatrices !
Hello
pour le calculer les équations des médianes du trinagle ABC, tu dois d'abord te dire que :
- une médiane passe par le milieu du coté et par le sommet opposé.
Ensuite tu traduis le tout à l'aide des vecteurs, je m'explique.
Calcul des coordonnées du point M, milieu de [AC] :
Xm = (Xa + Xc) / 2
Ensuite tu t'aides des formules de vecteurs :
tu calcule au préalable les cordonnées du vecteur AC et ceux de MB avec M(x;y)
tu fais alors : u scalaire v = xx' + yy' et tu reduis.
pour le calculer les équations des médianes du trinagle ABC, tu dois d'abord te dire que :
- une médiane passe par le milieu du coté et par le sommet opposé.
Ensuite tu traduis le tout à l'aide des vecteurs, je m'explique.
Calcul des coordonnées du point M, milieu de [AC] :
Xm = (Xa + Xc) / 2
Ensuite tu t'aides des formules de vecteurs :
tu calcule au préalable les cordonnées du vecteur AC et ceux de MB avec M(x;y)
tu fais alors : u scalaire v = xx' + yy' et tu reduis.
enfin pour l'équation du cercle, il te fo les coordonnées du centre cad celles du point d'intersection des médiatrices, puis le rayon qui est donné par la distance du centre du cercle à l'un des trois sommets du triangle ! la forme canonique de ce genre d'équation est rappelée ds le cour ! puis pour les intersections du cercle avec les axes du repère, tu poses successivement x=0 pour trouver les valeurs de y (o nombre de 2), puis idem en posant y=0 ! @ +
Salut,
J'ai un problème pour les équations. Dans mon cours il est noté que l'équation vectorielle d'une droite est d (3 barres les verticales alignées) OM=OA+kAB (kR)
Je ne comprends pas comment on fait cette équation car c'est bien une équation comme ca que je dois faire vu que je suis dans les vecteurs.
Faut-il donner une valleur réelle aux vecteurs OM,OA et AB?
Et sinon quand on me demande de calculer ||AB|| il faut betement mettre la longueur de ce segment en mesurant avec l'équerre?
Encore merci
PS:comment savoir si des points sont cocycliques?
J'ai un problème pour les équations. Dans mon cours il est noté que l'équation vectorielle d'une droite est d (3 barres les verticales alignées) OM=OA+kAB (kR)
Je ne comprends pas comment on fait cette équation car c'est bien une équation comme ca que je dois faire vu que je suis dans les vecteurs.
Faut-il donner une valleur réelle aux vecteurs OM,OA et AB?
Et sinon quand on me demande de calculer ||AB|| il faut betement mettre la longueur de ce segment en mesurant avec l'équerre?
Encore merci
PS:comment savoir si des points sont cocycliques?
Salut, une droite D passant par A de vecteur directeur directeur directeur 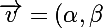) a une representation parametrique vectorielle:
a une representation parametrique vectorielle:
pour tout point il existe
il existe  tel que:
tel que:
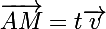 ou
ou 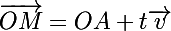
on utilise plutôt ,en geometrie analytique, une representation parametrique portant sur les coordonnées,t etant le parametre.
Ainsi,,\vec{v}(\alpha,\beta))}) a pour representation parametrique:
a pour representation parametrique:
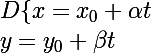

et on utilises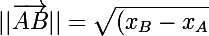^2+(y_B-y_A)^2)})
des points sont cocycliques lorsqu'ils appartiennent à un même cercle
pour tout point
on utilise plutôt ,en geometrie analytique, une representation parametrique portant sur les coordonnées,t etant le parametre.
Ainsi,
c'est la norme du vecteurEt sinon quand on me demande de calculer ||AB|| il faut betement mettre la longueur de ce segment en mesurant avec l'équerre?
et on utilises
comment savoir si des points sont cocycliques?
des points sont cocycliques lorsqu'ils appartiennent à un même cercle
Re, pour l'expression analytique il faut que tu exprimes les equations te tes droites en fonction de x et y
pour les points cocycliques si tu as ton equation de cercle tu peux verifier que les coordonnées de chaque points verifient la dite equation
sinon tu peux utiliser:
si ABCD sont 4 points, si (AB) et (CD) se coupent en M et si MA × MB = MC × MD (en mesures algébriques) alors les quatre points sont cocycliques.
....
pour les points cocycliques si tu as ton equation de cercle tu peux verifier que les coordonnées de chaque points verifient la dite equation
sinon tu peux utiliser:
si ABCD sont 4 points, si (AB) et (CD) se coupent en M et si MA × MB = MC × MD (en mesures algébriques) alors les quatre points sont cocycliques.
....
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
