Points sur un cercle.
15 messages
- Page 1 sur 1
Points sur un cercle.
Yo!
On prend A1...An n points sur le cercle unité ( de centre 0, de rayon 1)
Montrer que l'on peut trouver un point M sur ce cercle, tel que
MA1*MA2*...*MAn=1 (MA1 pris comme la distance de M à A1).
Bonne réflexion.
On prend A1...An n points sur le cercle unité ( de centre 0, de rayon 1)
Montrer que l'on peut trouver un point M sur ce cercle, tel que
MA1*MA2*...*MAn=1 (MA1 pris comme la distance de M à A1).
Bonne réflexion.
Notant z1,..,zn les complexes associés à A1,..,An, et posant P(z)=produit des (z-ak), le but est de montrer qu'il existe z de module 1 tel que |P(z)|=1. Or |P| s'annule aux ak donc par le théo des valeurs intermédiaires il suffit de montrer qu'il existe z de module 1 tel que |P(z)|>1. Plusieurs moyens de procéder pour montrer ça: l'analyse complexe permet par exemple de torcher par le principe du maximum en remarquant que |P(0)|=1.
(En fait ya meme moyen de manière plus efficace et plus élémentaire de montrer qu'il existe z de module 1 tel que |P(z)|>2)
(En fait ya meme moyen de manière plus efficace et plus élémentaire de montrer qu'il existe z de module 1 tel que |P(z)|>2)
Elémentaire ne veut pas forcément dire évident (tu en sais quelque chose^^)
Tu développes ton polynome:
=z^n+a_{n-1}z^{n-1}+\cdots+a_0)
où on sait que |a0|=1. Quitte à remplacer P(z) par P(cz)/c^n où c est un complexe de module 1 bien choisi, on peut supposer a0=1. Et maintenant l'astuce: on regarde la moyenne de P sur les racines n-iemes de l'unité. Si on les note u1,..,un, en utilisant les formules classiques
 si m divise n,0 sinon,
si m divise n,0 sinon,
on en déduit
=1+1=2)
et donc qu'il existe k tel que|\geq 2)
Tu développes ton polynome:
où on sait que |a0|=1. Quitte à remplacer P(z) par P(cz)/c^n où c est un complexe de module 1 bien choisi, on peut supposer a0=1. Et maintenant l'astuce: on regarde la moyenne de P sur les racines n-iemes de l'unité. Si on les note u1,..,un, en utilisant les formules classiques
on en déduit
et donc qu'il existe k tel que
Oui, l'intégrale est le plus naturel, mais c'est pas suffisamment efficace, ça donne juste la minoration par 1..A noter que la méthode de Le_chat, à savoir Parceval, donne déjà une minoration un peu mieux (racine(2))..Ce fut aussi ma première amélioration, et j'ai galéré un moment avant de trouver cette mino optimale (atteinte par z^n+1 par ex), par une méthode initialement très tordue (oui j'avoue, je n'ai pas torché ce truc en un jour, j'avais réfléchi sur ce problème ya quelques temps déjà)
Généralisant cette méthode, ça donne que si=a_nz^n+...+a_0) , alors la norme infinie de P sur le cercle se minore par
, alors la norme infinie de P sur le cercle se minore par  (avec cas d'égalité pour
(avec cas d'égalité pour =az^n+b) )
)
Autre fait intéressant, ça permet de retrouver un résultat classique: Si P est un poly réel unitaire, la norme infinie de P sur [-1,1] est supérieure à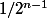 , avec cas d'égalité pour les polynomes de Tchebytchev (normalisés): Il suffit de remarquer que
, avec cas d'égalité pour les polynomes de Tchebytchev (normalisés): Il suffit de remarquer que
=P\left(\frac{1}{2}\left(e^{it}+\frac{1}{e^{it}}\right)\right)) , et qu'on en revient ainsi à minorer la norme infinie sur le cercle du polynome
, et qu'on en revient ainsi à minorer la norme infinie sur le cercle du polynome =z^nP\left(\frac{1}{2}\left(z+\frac{1}{z} \right)\right))
Généralisant cette méthode, ça donne que si
Autre fait intéressant, ça permet de retrouver un résultat classique: Si P est un poly réel unitaire, la norme infinie de P sur [-1,1] est supérieure à
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
