Bonjour,
J'ai lu sur beaucoup de différents sites / livres que l'intersection entre un ellipsoïde et un plan est toujours une ellipse, une point ou l'ensemble vide.
Ma question est : comment le démontrer ?
J'ai vu sur le net différentes démonstrations incluant un changement de repère. Mais, comme ce repère a la même origine que le repère de départ, cela signifie que le plan considéré passe par l'origine. Comme faire pour extrapoler à n'importe quel plan ?
Intersection plan et ellipsoide
6 messages
- Page 1 sur 1
analytiquement, tu as intérêt à prendre le repère assurant la symétrie de l'ellipsoïde
 (1)
(1)
dans ce repère, tout plan peut s'écrire
tu en tire en fonction de
en fonction de  et
et  et tu reportes dans (1)
et tu reportes dans (1)
tu développes en et
et  pour revenir à une forme classique de conique
pour revenir à une forme classique de conique

et tu montres que qui assure que c'est une ellipse
qui assure que c'est une ellipse
si l'ellipsoïde est de révolution, tu peux retrouver un cercle
dans ce repère, tout plan peut s'écrire
tu en tire
tu développes en
et tu montres que
si l'ellipsoïde est de révolution, tu peux retrouver un cercle
Bj
voici une preuve intrinsèque (qui n'utilise pas de repère)
J'adopte les définitions suivantes:
Dans un plan affine réel, une ellipse de centre O est une courbe dont l'équation est de la forme
q(OM) = k où q est une forme quadratique définie positive et k une constante > 0
(OM = vecteur OM)
Dans un espace affine réel de dimension 3, un ellipsoide de centre O est une surface dont l'équation est de la forme q(OM) = k où q est une forme quadratique définie positive et k une constante > 0
Soit donc un ellipsoide (S) de centre O d'équation q(OM) = k et un plan (P). Je note (C) la courbe d'intersection et b la forme bilinéaire symétrique associée à q.
La droite passant par O et b-orthogonale au plan (P) coupe ce plan (P)en U.
q(OM) = q(OU+UM) = b(OU+UM,OU+UM)=q(OU)+q(UM)+2b(OU,UM)
M est sur (C) ss q(OM) = k et M sur (P)
M est sur (P) ss b(OU,UM) = 0
finalement: M est sur (C) ss q(UM) = k - q(OU) et M sur (P)
conclusion: (C) est une ellipse (éventuellement réduite à un point) ou l'ensemble vide
voici une preuve intrinsèque (qui n'utilise pas de repère)
J'adopte les définitions suivantes:
Dans un plan affine réel, une ellipse de centre O est une courbe dont l'équation est de la forme
q(OM) = k où q est une forme quadratique définie positive et k une constante > 0
(OM = vecteur OM)
Dans un espace affine réel de dimension 3, un ellipsoide de centre O est une surface dont l'équation est de la forme q(OM) = k où q est une forme quadratique définie positive et k une constante > 0
Soit donc un ellipsoide (S) de centre O d'équation q(OM) = k et un plan (P). Je note (C) la courbe d'intersection et b la forme bilinéaire symétrique associée à q.
La droite passant par O et b-orthogonale au plan (P) coupe ce plan (P)en U.
q(OM) = q(OU+UM) = b(OU+UM,OU+UM)=q(OU)+q(UM)+2b(OU,UM)
M est sur (C) ss q(OM) = k et M sur (P)
M est sur (P) ss b(OU,UM) = 0
finalement: M est sur (C) ss q(UM) = k - q(OU) et M sur (P)
conclusion: (C) est une ellipse (éventuellement réduite à un point) ou l'ensemble vide
J'ai utilisé ta méthode el niala (mes cours sur les coniques datent un peu et j'avais oublié cette forme).
Donc,
Soit l'ellipsoide (E) d'équation (1)
(1)
Soit le plan (P) d'équation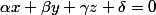 (2)
(2)
Les points formant l'intersection entre (E) et (P) appartiennent à ces deux courbes donc leurs coordonnées vérifient les deux équations.
A partir de (2), en supposant , on a
, on a

En remplaçant cette dernière dans (1), on a
^2}{c^2 \gamma^2} - 1 = 0)
- a^2 b^2 c^2 \gamma ^2 = 0)
 x^2 + 2 a^2 b^2 \alpha \beta x y + (a^2 c^2 \gamma^2 + a^2 b^2 \beta ^2) y^2 + 2 a^2 b^2 \alpha \delta x + 2 a^2 b^2 \beta \delta y + a^2 b^2 \delta^2 - a^2 b^2 c^2 \gamma ^2 = 0)
Cette équation est l'équation cartésienne d'une conique de discriminant
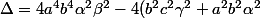(a^2 c^2 \gamma^2 + a^2 b^2 \beta ^2))
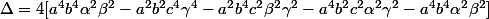
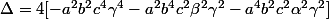
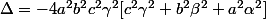
Comme on a supposé que est diiférent de zéro et que a, b et c le sont aussi, le premier terme n'est pas nul. Le deuxième terme est également différent de zéro car
est diiférent de zéro et que a, b et c le sont aussi, le premier terme n'est pas nul. Le deuxième terme est également différent de zéro car  et
et  .
.
Donc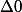 ,
,  et
et  ,
, 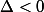
Supposons maintenant que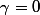 ,
, 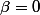 et
et 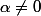
(2) devient


et (1) devient


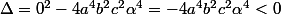
Supposons que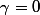 ,
, 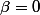 et
et 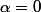
alors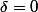 et (P) est l'ensemble vide. Comme toute intersection avec un ensemble vide est l'ensemble vide, l'intersection entre (P) et (E) est dans ce cas vide.
et (P) est l'ensemble vide. Comme toute intersection avec un ensemble vide est l'ensemble vide, l'intersection entre (P) et (E) est dans ce cas vide.
On peut ainsi en conclure que toute intersection entre un ellipsoide et un plan, est une ellipse, un point ou l'ensemble vide.
Tout est ok ?
Donc,
Soit l'ellipsoide (E) d'équation
Soit le plan (P) d'équation
Les points formant l'intersection entre (E) et (P) appartiennent à ces deux courbes donc leurs coordonnées vérifient les deux équations.
A partir de (2), en supposant
En remplaçant cette dernière dans (1), on a
Cette équation est l'équation cartésienne d'une conique de discriminant
Comme on a supposé que
Donc
Supposons maintenant que
(2) devient
et (1) devient
Supposons que
alors
On peut ainsi en conclure que toute intersection entre un ellipsoide et un plan, est une ellipse, un point ou l'ensemble vide.
Tout est ok ?
el niala a écrit:tu développes enet
pour revenir à une forme classique de conique
et tu montres quequi assure que c'est une ellipse
si l'ellipsoïde est de révolution, tu peux retrouver un cercle
Je viens de relire un cours et il semble que la forme soit
En tout cas, merci de l'indication :lol3:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
