Développement / factorisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sladix
- Messages: 5
- Enregistré le: 12 Oct 2006, 19:28
-
 par Sladix » 22 Jan 2012, 14:53
par Sladix » 22 Jan 2012, 14:53
Bonjour,
N'étant pas ce qu'on appelle une crème en maths, me voilà en train de galérer sur un corrigé.
Après un calcul de domaine sur R pour
+ln(x-2) <= ln(8x^2-8))
On arrive donc à
(x-2) <= (8x^2-8))
J'ai donc développé et ça donne
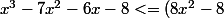)
=
 <= 0)
Alors que ça devrait faire
<=0)
J'en viens donc à penser que je comprends trop le développement/fact ..
Un peu d'aide serait la bienvenue !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Jan 2012, 15:21
par barbu23 » 22 Jan 2012, 15:21
Sladix a écrit:Bonjour,
N'étant pas ce qu'on appelle une crème en maths, me voilà en train de galérer sur un corrigé.
Après un calcul de domaine sur R pour
+ln(x-2) <= ln(8x^2-8))
On arrive donc à
(x-2) <= (8x^2-8))
J'ai donc développé et ça donne
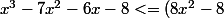)
=
 <= 0)
Alors que ça devrait faire
<=0)
J'en viens donc à penser que je comprends trop le développement/fact ..
Un peu d'aide serait la bienvenue !!
Bonjour : :happy3:
D'abord, tu dois justifier comment tu passes de :
+ln(x-2) \leq \ln(8x^2-8))
à
 (x-2) \leq 8x^2 -8)
.
Tu dis que

est croissante sur

, par conséquent :
(x-2))} \leq e^{\ln(8x^2-8)})
, d'où le résultat.
Pour ce qui est du développement de l'expression factorisée :
On a :
 (x-2) \leq 8x^2 -8)
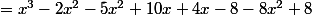
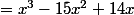
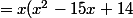 = 0 $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Jan 2012, 15:22
par barbu23 » 22 Jan 2012, 15:22
Sladix a écrit:Bonjour,
N'étant pas ce qu'on appelle une crème en maths, me voilà en train de galérer sur un corrigé.
Après un calcul de domaine sur R pour
+ln(x-2) <= ln(8x^2-8))
On arrive donc à
(x-2) <= (8x^2-8))
J'ai donc développé et ça donne
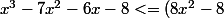)
=
 <= 0)
Alors que ça devrait faire
<=0)
J'en viens donc à penser que je comprends trop le développement/fact ..
Un peu d'aide serait la bienvenue !!
Bonjour : :happy3:
D'abord, tu dois justifier comment tu passes de :
+ln(x-2) \leq \ln(8x^2-8))
à
 (x-2) \leq 8x^2 -8)
.
Tu dis que

est croissante sur

, par conséquent :
(x-2))} \leq e^{\ln(8x^2-8)})
, d'où le résultat.
Pour ce qui est du développement de l'expression factorisée :
On a :
 (x-2) \leq 8x^2 -8)
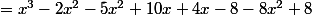
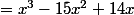
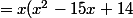 = 0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
