Bonsoir, je suis une second et j'ai reçus un DM de mathématiques Niveau Première. Le problème :mur: c'est que moi et les Maths ... :hein: ... Bref Je suis avec une camarade et je n'ai vraiment envie qu'elle se prennent un carton à cause de moi ( je n'essaye pas de me justifier ^^' ) Je bloque sur deux ... chose Voici l'énoncer :
En déduire la valeur de la somme de
S= 1/1x2 + 1/2x3 + 1/3x4 + ... + 1/ 2000x2001
puis la second énoncer :
Écrire simplement, en fonction de n la somme
T= 1/1x2 + 1/2x3 + 1/3x4+ ... + 1/nx(n+1)
Voilà :help: Merci en tout cas !!!
Exercice niveau Première S
6 messages
- Page 1 sur 1
Bonsoir,
En déduire signifie que tu dois utiliser ce qui a été démontré dans la ou les questions précédentes. Où sont-elles ?
Tu as écrit
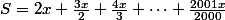
ou peut-être
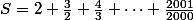 .
.
En tout cas je suspecte que ce n'est ni l'un ni l'autre et que tu dois révoir ton cours de cinquième sur les priorités; pour calculer un produit sans parenthèse, on effectue les calculs de la gauche vers la droite et non de la droite vers la gauche comme tu sembles le croire.
Je t'invite donc à réécrire correctement S.
OpheDite a écrit: En déduire la valeur de la somme de
En déduire signifie que tu dois utiliser ce qui a été démontré dans la ou les questions précédentes. Où sont-elles ?
S= 1/1x2 + 1/2x3 + 1/3x4 + ... + 1/ 2000x2001
Tu as écrit
ou peut-être
En tout cas je suspecte que ce n'est ni l'un ni l'autre et que tu dois révoir ton cours de cinquième sur les priorités; pour calculer un produit sans parenthèse, on effectue les calculs de la gauche vers la droite et non de la droite vers la gauche comme tu sembles le croire.
Je t'invite donc à réécrire correctement S.
OpheDite a écrit:la second énoncer :
Écrire simplement, en fonction de n la somme
T= 1/1x2 + 1/2x3 + 1/3x4+ ... + 1/nx(n+1)
Salut !
Je suppose que T s'écrit ainsi :
Démontre qu'il existe deux réels
Ecris autrement, grâce à cette relation, les expressions :
-
-
-
...
-
Puis tu additionnes toutes ces lignes pour obtenir quelque chose qui s'arrange.
:++:
Pendant que je le vois, cela devrait également te permettre de répondre à ta première question bien qu'il faille "déduire", mais comme on n'a pas le début...
Dinozzo13 a écrit:Salut !
Je suppose que T s'écrit ainsi :.
Démontre qu'il existe deux réelset
tels que :
.
Ecris autrement, grâce à cette relation, les expressions :
-
-
-
...
-
Puis tu additionnes toutes ces lignes pour obtenir quelque chose qui s'arrange.
:++:
Pendant que je le vois, cela devrait également te permettre de répondre à ta première question bien qu'il faille "déduire", mais comme on n'a pas le début...
OpheDite a écrit:Bonsoir, je suis une second et j'ai reçus un DM de mathématiques Niveau Première. Le problème :mur: c'est que moi et les Maths ... :hein: ... Bref Je suis avec une camarade et je n'ai vraiment envie qu'elle se prennent un carton à cause de moi ( je n'essaye pas de me justifier ^^' ) Je bloque sur deux ... chose Voici l'énoncer :
En déduire la valeur de la somme de
S= 1/1x2 + 1/2x3 + 1/3x4 + ... + 1/ 2000x2001
puis la second énoncer :
Écrire simplement, en fonction de n la somme
T= 1/1x2 + 1/2x3 + 1/3x4+ ... + 1/nx(n+1)
Voilà :help: Merci en tout cas !!!
Bonjour,
Fibonacci:
somme(p=1 à 2000)(2000*2001/(n)(n+1))/2000*2001=somme(p=1 à 2000) 1/(n)(n+1)=somme(p=1 à 2000)(1 - 1/p)=1-1/2001=2000/2001
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
