Exercice nombres complexes

[Atlantos]

Bonjour, je suis face à un exercice que je n'arrive pas. En fait, je dois "Interpreter géométriquement (et en justifiant) le module et l'argument de z' "
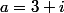
Sachant que je je possede les points A et B d'affixe et
Et qu'à tout point M d'affixe z n'est pas égal a b, on associe M' d'affixe

Quelqu'un a une idée ?

[albukerk]

Bonjour, je suis face à un exercice que je n'arrive pas. En fait, je dois "Interpreter géométriquement (et en justifiant) le module et l'argument de z' "
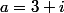
Sachant que je je possede les points A et B d'affixe et
Et qu'à tout point M d'affixe z n'est pas égal a b, on associe M' d'affixe

Quelqu'un a une idée ?

Soient z(a) l'affixe du point A et z(b) l'affixe du point B, alors on a :

z'= z-z(a) / z-z(b)

Or module de z-z(a) = AM De même que z-z(b) = BM D'où module de z' = AM/BM

Le même raisonnement avec les arguments.

[Atlantos]

La deuxième question pose aussi quelques problèmes, " Déterminer l'ensemble des points M tels que z' soit un imaginaire pur"

Il faut certainement pour cela "éliminer" les partie réel du dénominateur et du numérateur. Cependant étant donnée qu'on utilise une méthode géométrique doit on procéder comme cela ?

[albukerk]

La deuxième question pose aussi quelques problèmes, " Déterminer l'ensemble des points M tels que z' soit un imaginaire pur"

Il faut certainement pour cela "éliminer" les partie réel du dénominateur et du numérateur. Cependant étant donnée qu'on utilise une méthode géométrique doit on procéder comme cela ?

Donc qu'on parlde partie réelle et imaginaire, tu dois poser z = x+ iy.

Après, tu developpes le tout, et tu sépares les deux parties.

Ensuite, un nombr et un imaginaire pur ssi sa partie imaginaire existe et que sa parie réelle est nulle.

[Carpate]

La deuxième question pose aussi quelques problèmes, " Déterminer l'ensemble des points M tels que z' soit un imaginaire pur"

Il faut certainement pour cela "éliminer" les partie réel du dénominateur et du numérateur. Cependant étant donnée qu'on utilise une méthode géométrique doit on procéder comme cela ?

Il faut conserver la méthode géométrique :
z' imaginaire pur : son argument vaut +/- pi/2