Bonjour,
mon fils a un exercice de mathématique, et je voudrais pouvoir l'aider un peu à comprendre et lui expliquer aussi, voici l'exercice :
Soit l'expression E = (2x + 1 )³ - (-3x + 5)² (2x + 1)
Développer, puis réduire E.
On pourra remarquer que (2x + 1 )³ = (2x + 1)(2x + 1)²
d'avance merci pour votre aide
Exercice de développement
3 messages
- Page 1 sur 1
Pour développer on utilise les formules suivantes :
(a + b) (c + d) = ac + ad + bc + bd
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
E = (2x + 1 )³ - (-3x + 5)² (2x + 1)
= (2x + 1)(2x + 1)² - (-3x + 5)² (2x + 1)
= (2x+1)(.................) - (..................) (2x + 1)
puis on développe (2x+1) par rapport à (.......................) et (2x+1)par rapport à (.......................)
(a + b) (c + d) = ac + ad + bc + bd
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
E = (2x + 1 )³ - (-3x + 5)² (2x + 1)
= (2x + 1)(2x + 1)² - (-3x + 5)² (2x + 1)
= (2x+1)(.................) - (..................) (2x + 1)
puis on développe (2x+1) par rapport à (.......................) et (2x+1)par rapport à (.......................)
Bonjour,
Ainsi,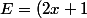(2x+1)^2-(-3x+5)^2 (2x+1)) .
.
On peut procéder de plusieurs façons :
Ainsi,
On peut procéder de plusieurs façons :
- développer les parenthèses au carré en reconnaissant des identités remarquables ;
- factoriser E par un facteur commun puis développer la seconde parenthèse en reconnaissant une identité remarquable.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
