Vecteurs colinéaires merci !

[the-one]

Bonsoir,

J'ai un exercice sur la trigonométrie a faire.
:go: http://www.casimages.com/img.php?i=111230114132502665.jpg

Je bloque a la 3ème question, j'aimerais bien de l'aide pour prouver la colinéarité.
Ca fait bien une bonne demi heure que je bloque, je deviens fou :mur:

Merci beaucoup ...

[el niala]

36 façons d'y parvenir, en particulier en utilisant :
- la symétrie de B et E (et C et D) par rapport à (OA)
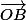
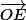
- les projections de et sur les axes

[the-one]

36 façons d'y parvenir, en particulier en utilisant :
- la symétrie de B et E (et C et D) par rapport à (OA)
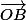
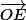
- les projections de et sur les axes

C'est peut etre qu'il est tard, mais ça ne m'eclaire pas beaucoup :hum:

[el niala]

par les projections sur les axes :





conclusion ?

[the-one]

(ob + Oe) = 0 = Oa ?

[el niala]

(ob + Oe) = 0 = Oa ?

non, ce sont seulement les composantes sur l'axe perpendiculaire à (OA) qui s'annulent