Résolu :)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 10:21
par Reduel » 30 Déc 2011, 10:21
Bonjour, pour la rentrée j'ai un petit exercice à faire mais je bloque à une question.
Il faudra résoudre : f'(a)=m
Or f'(a)= 4/(a-2)².
Donc on aurait à résoudre l'équation 4(a-2)²=m
Moi je trouve a=-(m²-4m+(4m/a)-(4/a).
Mais cela me parait assez complexe comme solution.
Pouvez vous m'aider ? :)
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 30 Déc 2011, 10:55
par maths0 » 30 Déc 2011, 10:55
J'aurais plutôt tendance à dire que:
}^2}}}\\ {\left( {a - 2} \right)^2}m = 4\\ m{a^2} - 4a + 4 = 4\\ m{a^2} - 4a = 0\\ m = \frac{{4a}}{{{a^2}}}\\ m = \frac{4}{a} \end{array})
?
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 10:57
par Reduel » 30 Déc 2011, 10:57
Es-tu sur que (a-2)²m= ma²-4a+4?
Ca ne serait pas plutot : ma²-4am+4m ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 30 Déc 2011, 11:00
par maths0 » 30 Déc 2011, 11:00
Oui je fais n'importe quoi :ptdr:
^2}m = 4\\ m{a^2} - 4a + 4m = 4\\ m\left( {{a^2} + 4} \right) = 4 - 4a\\ m = \frac{{4 - 4a}}{{\left( {{a^2} + 4} \right)}} \end{array})
?
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 11:03
par Reduel » 30 Déc 2011, 11:03
Mais moi il faut que je trouve a et non m. :help:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 30 Déc 2011, 11:13
par maths0 » 30 Déc 2011, 11:13
Tu peux le dire que j'écris n'importe quoi

}^2}}}\\<br />m{\left( {a - 2} \right)^2} = 4\\<br />m{a^2} - 4am + 4m = 4\\<br />\left( m \right){a^2} + \left( { - 4m} \right)a + \left( {4m - 4} \right) = 0<br />\end{array})
Calcul du discriminant ..
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 11:20
par Reduel » 30 Déc 2011, 11:20
Je suis arrivé également au meme résultat que toi. Mais après je ne comprend pas comment trouver a=... :hum:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 30 Déc 2011, 11:21
par maths0 » 30 Déc 2011, 11:21
Tu as déjà vu la résolution d'un trinôme de la forme f(x)=ax²+bx+c ?
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 11:24
par Reduel » 30 Déc 2011, 11:24
Oui.
Attend oui j'ai vu je crois.
Je te dis me résultats dans 5min ;)
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 11:48
par Reduel » 30 Déc 2011, 11:48
maths0 a écrit:Tu as déjà vu la résolution d'un trinôme de la forme f(x)=ax²+bx+c ?
Alors, si je n'ai pas été mauvais:

Delta: 16m²-16m²+16m=16m
Donc si m0, alors a a deux solutions.
a1= (4m-4rac(m)) / 2m
a2= (4m+4rac(m=)) / 2m
Cest ca ?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 30 Déc 2011, 11:49
par maths0 » 30 Déc 2011, 11:49
Je crois bien

^2} - 4\left( m \right)\left( {4m - 4} \right)\\ \Delta = 16{m^2} - 16{m^2} + 16m\\ \Delta = 16m\\ {a_1} = \frac{{4m - 4\sqrt m }}{{2m}} = \frac{{4m}}{{2m}} - \frac{{4\sqrt m }}{{2m}} = 2 - 2\frac{{\sqrt m }}{m}\\ {a_2} = \frac{{4m + 4\sqrt m }}{{2m}} = 2 + 2\frac{{\sqrt m }}{m} \end{array})
-
Reduel
- Messages: 9
- Enregistré le: 30 Déc 2011, 10:15
-
 par Reduel » 30 Déc 2011, 11:51
par Reduel » 30 Déc 2011, 11:51
maths0 a écrit:Attention pour tes intervalles à revoir car delta=16m

^2} - 4\left( m \right)\left( {4m - 4} \right)\\ \Delta = 16{m^2} - 16{m^2} + 16m\\ \Delta = 16m\\ {a_1} = \frac{{4m - 4\sqrt m }}{{2m}} = \frac{{4m}}{{2m}} - \frac{{4\sqrt m }}{{2m}} = 2 - 2\frac{{\sqrt m }}{m}\\ {a_2} = \frac{{4m + 4\sqrt m }}{{2m}} = 2 + 2\frac{{\sqrt m }}{m} \end{array})
Cela si m positif non ? Car a1 et a2 sont valabes seulement si Delta est positif.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 30 Déc 2011, 16:51
par Sa Majesté » 30 Déc 2011, 16:51
Si m est négatif alors léquation 4/(a-2)²=m, d'inconnue réelle a, n'admet pas de solution puisque 4/(a-2)² est strictement positif
Si m est strictement positif alors on peut écrire
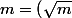^2)
et résoudre l'équation
^2-\left(\frac{2}{a-2}\right)^2 = 0)
en factorisant avec l'identité remarquable A²-B² = (A-B)(A+B)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
