salut ! :we:
j'ai rencontre un probleme dans la resolution d'une question dans cet exercice
1)a) pour tout entier

, montrer qu'il existe un polynome
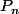
tel que

(x)=\frac{P_{n}(x)}{(1-x^2)^(n-\frac{1}{2})})
,montrer ensuite que pour

>=

, le polynome
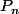
est unique.
b) verifier,pour tout

,l'egalite :
arcsin''(x)=x arcsin'(x))
, en deduire que pour tout

, on a l'egalite polynomiale;
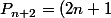XP_{n+1}+n^{2}(1-X^2)P_{n})
c) en deduire que la fonction

est un element de
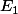
avec
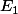
l'ensemble de fonction

de classe infini ,a valeur dans

et

,

:
(x) >= 0)
2-a) A l'aide de relation polynomiale de 1-b) determiner une expression simplifiee de
)
pour tout entier

>=

en deduire explicitement
(0))
pour tout entier

b) determiner en primitivant un DL usuel au voisinage de

, un DL a tout ordre de la fonction

au voisinage de

, retrouver alors
(0))
pour tout entier

il y a d'autre question mais ce que j'arive pas a prouver est 2-a) . j'ai trouver que
(0)=\frac{n^2}{n+1} P_{n}(0))
le probleme est comment trouver
)
j'ai deja trouver que
=\frac{P''_{n}(0)}{(n-1)^2})
mais ca sert a rien
merci pour votre aide :lol3:
