Implication

par **kokorico06** » 21 Déc 2011, 13:57

Bonjour,

j'ai un exercice que je ne comprend pas, pourriez vous m'aider?

Le voici:

Soit e appartenant à R+*, trouver un n (éta) appartenant à R+* de sorte que |x-1| <= n IMPLIQUE
|((x+1)/(x²+1)) - 1|<= e

Merci de votre aide !

par **mathelot** » 21 Déc 2011, 14:15

bonjour,

Avec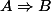

,A est une condition suffisante de B et B est une condition
nécessaire de A.

Dans le cas présent, tu peux supposer en plus que

, ce qui permet un encadrement de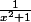

ce qui revient à écrire que

est une condition suffisante
pour obtenir la conclusion de l'implication (mais pas une condition nécessaire)

par **kokorico06** » 21 Déc 2011, 14:37

Mais pourquoi on devrait supposer que x appartient à [0; 2] ?

par **Doraki** » 21 Déc 2011, 15:58

Si e=3 tu peux trouver un ;) qui convient ?

par exemple tu peux montrer que si |x-1|<2 alors |(x+1)/(x²+1)-1|<3 ?

par **mathelot** » 22 Déc 2011, 00:34

kokorico06 a écrit:Mais pourquoi on devrait supposer que x appartient à [0; 2] ?

on doit pas. c'est une condition suffisante pour donner un encadrement
mais pas une condition nécessaire

par **cheria2010** » 22 Déc 2011, 13:23

salut
en peu encadrer

tel que

trouve le facteur

dans

par **kokorico06** » 22 Déc 2011, 18:59

Salut,

((x+1)/(x²+1)) - 1 = -x(x-1)/(x²+1)

or on a déjà un encadrement de |x-1| donc il nous reste a trouver un encadrement pour |(-x)/(x²+1)|
et c'est la que je bloque !!

Merci de votre aide.

par **kokorico06** » 22 Déc 2011, 19:02

Cheria2010 je ne comprend pas pk tu dis que eta appartient à [0;1]

pck |x-1| <= eta équivaut à : - eta <= x-1 <= eta équivaut à : 1 - eta <= x <= 1+eta

Mais après je ne sais pas quoi faire

Implication

implication

Qui est en ligne