Probléme démonstration trigonometrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
roach
- Messages: 3
- Enregistré le: 03 Déc 2010, 16:04
-
 par roach » 16 Déc 2011, 10:45
par roach » 16 Déc 2011, 10:45
Salut voici un problème que j' ai eu à un examen de math .
Si a+b+c+d= 2
 Démontre que
Démontre quesina+sinb+sinc+sind= 4sin a+b/2 sin b+c/2 sin a+c/2
:mur:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 16 Déc 2011, 13:00
par Ericovitchi » 16 Déc 2011, 13:00
Bonjour, déjà il faudrait faire attention aux parenthèses :
sina+sinb+sinc+sind= 4sin ((a+b)/2) sin ((b+c)/2) sin ((a+c)/2 )
il faut certainement faire un usage judicieux de la formule
sin p + sin q = 2sin((p+q)/2)sin(((p-q)/2)
Commence par remplacer d par 2Pi -(a+b+c) tu te ramènes à traiter sina+sinb+sinc-sin(a+b+c)
puis tu emploies la formule sur les deux premiers termes
sin(a)+sin(b)= 2sin((a+b)/2)sin(((a-b)/2) et sur les deux autres
sin(c)-sin(a+b+c)=-2 sin((a+b)/2) cos(a/2+b/2+c)
tu mets 2sin((a+b)/2) en facteur et tu transforme le second facteur qui est une somme en produit, et tu devrais tomber sur la formule finale.
-
romani01
- Membre Relatif
- Messages: 226
- Enregistré le: 04 Nov 2011, 01:04
-
 par romani01 » 19 Déc 2011, 00:07
par romani01 » 19 Déc 2011, 00:07
Salut.
Ericovitchi a voulu écrire
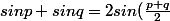cos(\frac{p-q}{2}))
.
-
roach
- Messages: 3
- Enregistré le: 03 Déc 2010, 16:04
-
 par roach » 19 Déc 2011, 13:29
par roach » 19 Déc 2011, 13:29
Merci beaucoup pour votre aide .

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 19 Déc 2011, 15:25
par Ericovitchi » 19 Déc 2011, 15:25
oui tu as raison, je me suis trompé dans la formule sin(p)+sin(q) , merci d'avoir rectifié romani01
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités