Bonjour,
Je suis nouveau sur le forum et j'écris ce message parce que j'ai besoin d'aide au sujet d'une convergence $L^1$. Le problème est le suivant:
Etant donnée une suite $X_n$ de variables aléatoires (positives) telle que $nX_n$ converge en probabilité vers 0. Est-il vrai que l'espérance de $X_n$ est finie et qu'elle est uniformément bornée en $n$? (c'est-à-dire que \sup_{n}E[X_n] est fini). Il s'agit d'une question que je me suis posée et je n'ai aucune idée de la réponse.
J'attends vos réponses.
Bien à vous et bien cordialement,
Stalinou.
Convergence en probabilité et majoration de l'espérance
4 messages
- Page 1 sur 1
Ici, on peut prendre une variable aléatoire non intégrable, puisque tu veux un exemple à densité on peut prendre la loi de Cauchy, de densité =\frac 1{\pi(1+x^2)}) , qui n'est pas intégrable. On prend
, qui n'est pas intégrable. On prend  une variable aléatoire de densité
une variable aléatoire de densité ) si
si 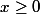 (pour avoir
(pour avoir  positive),
positive),  sinon, puis on pose
sinon, puis on pose  . On a la convergence presque sûre vers
. On a la convergence presque sûre vers  , donc en probabilités, mais
, donc en probabilités, mais  n'est pas intégrable.
n'est pas intégrable.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
