Problème d'analyse Concours TSIM
31 messages
- Page 1 sur 2 - 1, 2
Problème d'analyse Concours TSIM
Bonjour à tous,
j'ai un petit problème avec un exercice d'analyse issu d'annales du concours de Technicien Supérieur de l'Industrie et des Mines.
La fonction est : f(x)=((e(x))-1)/((e(x))+1)
je ne sais pas si j'ai le droit de mettre le lien internet du problème, pour que la formule soit plus claire, donc dans le doute je ne la mets pas.
Il est demandé de déterminer les limites de la fonction, établir le tableau de variation et de donner l'équation de la tangente à la courbe (C) en x=0. (je trouve g(x)=x/2)
Jusque là tout va bien.
Par contre ça se gâte lorsqu'on me demande d'étudier la position relative de la tangente par rapport à (C). Je pense savoir qu'il faut déterminer le signe de f(x)-g(x) mais c'est là que je bloque ...
Qqn pourrait m'aider ?
j'ai un petit problème avec un exercice d'analyse issu d'annales du concours de Technicien Supérieur de l'Industrie et des Mines.
La fonction est : f(x)=((e(x))-1)/((e(x))+1)
je ne sais pas si j'ai le droit de mettre le lien internet du problème, pour que la formule soit plus claire, donc dans le doute je ne la mets pas.
Il est demandé de déterminer les limites de la fonction, établir le tableau de variation et de donner l'équation de la tangente à la courbe (C) en x=0. (je trouve g(x)=x/2)
Jusque là tout va bien.
Par contre ça se gâte lorsqu'on me demande d'étudier la position relative de la tangente par rapport à (C). Je pense savoir qu'il faut déterminer le signe de f(x)-g(x) mais c'est là que je bloque ...
Qqn pourrait m'aider ?
ok !
je ne savais pas que j'avais le droit de mettre le lien :
http://www11.minefi.gouv.fr/metiers-concours/aidesprepa/adm_centrale/annales/tech_sup_im_ext/annales_tsim_externe_2011_maths.pdf
je ne savais pas que j'avais le droit de mettre le lien :
http://www11.minefi.gouv.fr/metiers-concours/aidesprepa/adm_centrale/annales/tech_sup_im_ext/annales_tsim_externe_2011_maths.pdf
ce n'est pas le sujet que tu as envoyé, mais un lien, je crois savoir que c'est peu apprécié, mais comme tu es presque au bout de l'exercice 1, on peut le terminer ici, en revanche pour les autres, mieux vaudrait que tu ouvres un nouveau topic
je suppose que 6) ne te pose pas de difficultés, ni même 7) -pense à la symétrie pour gagner du temps- 8) il te faut intégrer f, pense à l'astuce suivante :
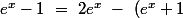)
je suppose que 6) ne te pose pas de difficultés, ni même 7) -pense à la symétrie pour gagner du temps- 8) il te faut intégrer f, pense à l'astuce suivante :
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
