Primitive de logarithme

[Atlantos]

Bonsoir, je dois trouver la primitive de la fonction f(x)=
sachant qu'on ma donné g(x)= et g'(x)=
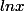
Pouvez vous m'aider à trouver cette primitive ?


amicalement,

[el niala]

évite d'écrire LA primitive, car en l'absence d'autre indication, il en existe une infinité, donc c'est UNE primitive

on t'a donné une primitive de ln(x)

tu connais une primitive de 1/x

tu remarques que (ln(x))/x est de la forme u'u avec u=ln(x)

[zorrg]

évite d'écrire LA primitive, car en l'absence d'autre indication, il en existe une infinité, donc c'est UNE primitive

on t'a donné une primitive de ln(x)

tu connais une primitive de 1/x

tu remarques que (ln(x))/x est de la forme u'u avec u=ln(x)

J'ai le même problème, et je suis allé jusque là mais je ne vois pas comment primitiver une fonction de la forme u'u...???

[maths0]

Je ne vois pas où est le problème.