Et dans notre cas que représente z' ?
Merci de répondre à mes questions :)
Nombre complexe.
29 messages
- Page 2 sur 2 - 1, 2
Comme je l'ai dit, c'est juste une notation pour désigner un deuxième complexe. J'aurais pû l'appeler x, t, q, bidule, je l'ai appelé z' (qui se lit "z prime"), c'est une notation mathématique conventionnelle.
Mais si ça te perturbe remplace le par n'importe quoi qui te convient mieux. La formule dit juste que le module d'un produit de deux complexes est le produit des modules de ces complexes.
Par exemple, |i*(2+i)|=|i|*|2+i|=1*sqrt(2²+1²)=sqrt(5)
Mais si ça te perturbe remplace le par n'importe quoi qui te convient mieux. La formule dit juste que le module d'un produit de deux complexes est le produit des modules de ces complexes.
Par exemple, |i*(2+i)|=|i|*|2+i|=1*sqrt(2²+1²)=sqrt(5)
Non, je ne suis pas d'accord, même si c'est vrai, encore une fois, c'est par coïncidence.
Ce qui est vrai, c'est que rac(a²+b²)*rac(a²+b²)=(rac(a²+b²))²=a²+b² et non ce que tu as écrit (la différence est fine, mais c'est elle qui fait tout!)
La formule que je voulais te faire utiliser est : |z²|=|z|²
Donc si z=a+ib, |z|=rac(a²+b²) et donc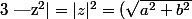^{2}=a^{2}+b^{2})
Ce qui est vrai, c'est que rac(a²+b²)*rac(a²+b²)=(rac(a²+b²))²=a²+b² et non ce que tu as écrit (la différence est fine, mais c'est elle qui fait tout!)
La formule que je voulais te faire utiliser est : |z²|=|z|²
Donc si z=a+ib, |z|=rac(a²+b²) et donc
29 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
