La fameuse zeta
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 29 Nov 2011, 18:51
par cheria2010 » 29 Nov 2011, 18:51
salut tout le monde
il une relation entre la fonction zeta

et la partie entiere [ ].
= s\int_1^{+\infty}\frac{[x]}{ x^{s +1 }}dx)
.
pouvez vous m'aider comment je peux trouver cette relation ....
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 29 Nov 2011, 18:56
par ffpower » 29 Nov 2011, 18:56
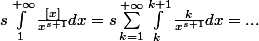
.
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 29 Nov 2011, 19:36
par cheria2010 » 29 Nov 2011, 19:36
ffpower a écrit: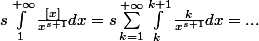
.
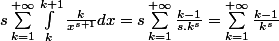
est-ce vrais ..
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 29 Nov 2011, 20:35
par Skullkid » 29 Nov 2011, 20:35
Salut, tu as mal calculé l'intégrale.
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 30 Nov 2011, 14:18
par cheria2010 » 30 Nov 2011, 14:18
Skullkid a écrit:Salut, tu as mal calculé l'intégrale.
salut .
c'est vrais mon calcul est faux .merci .
^s}])
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 30 Nov 2011, 14:22
par ffpower » 30 Nov 2011, 14:22
Ca a l'air mieux

Du coup, là reste plus qu'à faire une sommation d'Abel, remarquant que
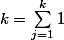
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 30 Nov 2011, 15:12
par cheria2010 » 30 Nov 2011, 15:12
merci de votre aide
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 04 Déc 2011, 09:38
par cheria2010 » 04 Déc 2011, 09:38
salut tout le monde
j'ai applique la formule de sommation d'Abel sur la somme :
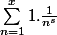
la formule de sommation est :
= A(x)f(x)-\int_1^x A(u)f'(u)du)
on pose
=\sum_1^x 1=[x]\ ,\ f(x)= \frac{1}{x^s} \ \ / x\in{R})
en trouve la formule lorsque x tend vers l'infini :
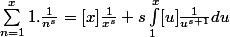
=s\int_1^{+\infty} \frac{[u]}{u^{s+1}}du)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités