Calcul de sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mezame
- Membre Naturel
- Messages: 10
- Enregistré le: 03 Nov 2009, 20:45
-
 par Mezame » 27 Nov 2011, 20:15
par Mezame » 27 Nov 2011, 20:15
Bonjour,
Dans le cadre d'un exercice, je dois effectuer un calcul de somme qui me donne un peu de fil à retordre...
Je vous expose le problème.
On a :
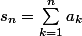
et

De plus,
}{\sum_{k=1}^{n} ka_{k}})
.
Et on me demande de prouver que
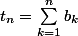
Seulement, voilà je ne cesse de tourner en rond sans obtenir le résultat attendu.
Je vous serais donc très reconnaissant si vous acceptiez de m'aider.

En vous remerciant d'avance,
Mezame.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 27 Nov 2011, 20:19
par Le_chat » 27 Nov 2011, 20:19
Salut. A vue de nez, il faudrait déjà essayer de manipuler l'expression de bk.
Par exemple, tu peux écrire ak=sk-s(k-1) et voir ce que ça te donne.
-
Mezame
- Membre Naturel
- Messages: 10
- Enregistré le: 03 Nov 2009, 20:45
-
 par Mezame » 27 Nov 2011, 20:22
par Mezame » 27 Nov 2011, 20:22
Merci pour cette réponse très rapide ! :)
J'edsaye immédiatement.
-
Mezame
- Membre Naturel
- Messages: 10
- Enregistré le: 03 Nov 2009, 20:45
-
 par Mezame » 27 Nov 2011, 20:35
par Mezame » 27 Nov 2011, 20:35
En testant la méthode que vous m'avez proposé, je dois avouer que je bloque rapidement.
J'ai substituer s(k)-s(k-1) à a(k) dans l'expression de b(k), mais je dois alors calculer la sommes des termes en k*s(k), ce qui me pose également quelques problèmes... :(
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 27 Nov 2011, 22:42
par Le_chat » 27 Nov 2011, 22:42
Justement, ce que tu dois faire c'est en quelque sorte une "transformation d'abel".
Il faut que écrives: Somme des k*ak=somme des k*(sk-s(k-1))=somme des k*sk-somme des k*s(k-1)
et faire une changement d'indice dans la seconde somme pour se ramener à une somme avec des sk et plus des s(k-1). Fais bien attention aux bornes!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
