Bonjour,
J'aimerais convertir en décimal le nombre binaire périodique suivant. Précisément, je veux obtenir 8 chiffres, après la virgule, en décimal, mais je ne parviens pas à obtenir la réponse, qui est, en décimal : 0,85693359
Le nombre binaire à convertir est : 0,1101
Noter que la période constitue les trois derniers chiffres, soit 101
Merci pour l'aide
Conversion en décimal de nombres binaires
12 messages
- Page 1 sur 1
Daniel55936 a écrit:Bonjour,
J'aimerais convertir en décimal le nombre binaire périodique suivant. Précisément, je veux obtenir 8 chiffres, après la virgule, en décimal, mais je ne parviens pas à obtenir la réponse, qui est, en décimal : 0,85693359
Le nombre binaire à convertir est : 0,1101
Noter que la période constitue les trois derniers chiffres, soit 101
Merci pour l'aide
T'es sûr de 0.85693....?
0.85693359 est la bonne réponse :-)
nodjim a écrit:T'es sûr de 0.85693....?
Bonjour,
La réponse est exacte, j'ai finalement réussi le calcul. J'ai obtenu cette réponse exacte de cette façon :
1 X 2*^-1 + 1 X 2^-2 + 0 X 2^-3 + 1 X 2^-4 +
1 X 2^-5 + 0 X 2^-6 + 1 X 2^-7 +
1 X 2^-8 + 0 X 2^-9 + 1 X 2^-10 +
1 X 2^-11
0,1101= 0.85693359
rappel, j'ai souligné la période. Du reste, la barre doit aller au-dessus, comme vous le savez
Merci pour votre aide, j'apprécie énormément!
Merci pour votre réponse !
eloudie06 a écrit:Le chiffre des unités correspond à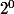
Celui des dizaines à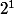
Celui des centaines à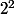
Par exemple 101 = 1*+0*
+1*
Donc tu fais pareil avec les chiffres après la virgule,,
...
Merci pour votre réponse :lol3:
Bonne réponse :-)
eloudie06 a écrit:En sommant jusqu'àj'obtiens 0.856934
Il s'agit en effet de la bonne méthode. En vous remerciant énormément pour l'aide
fournie.
Cordialement,
Daniel
Précision décimale
nodjim a écrit:Jusqu'à -11 on est encore assez loin de la précision décimale à 8 chiffres.
Bonjour,
D'après mes calculs, ces chiffres sont très précis. J'ai calculé jusqu'à -12, ou plus, pour obtenir cette certitude.
Merci encore pour votre aide précieuse.
Cordialement,
Daniel
Daniel55936 a écrit:Bonjour,
D'après mes calculs, ces chiffres sont très précis. J'ai calculé jusqu'à -12, ou plus, pour obtenir cette certitude.
Merci encore pour votre aide précieuse.
Cordialement,
Daniel
Toujours pas d'accord, pour moi je reste sur la valeur 6/7, sauf si on m'explique où je me suis trompé...
Daniel55936 a écrit:Le nombre binaire à convertir est : 0,1101
Noter que la période constitue les trois derniers chiffres, soit 101
Déja 0.1 101 101 101....=0.110 110 110......
la période est plutôt 110 non ? car elle commence dès le 1er chiffre après la virgule.
Maintenant si ce nombre est B, calculez 8B-B (8 en binaire s'écrit 1000, donc déplace la virgule de 3 rangs vers la droite): Je trouve 110=6
comme 8B-B=7B=6
B=6/7.
Maintenant 6/7 à une période 6. Combien de puissances de 2 faut il calculer pour trouver la période en binaire ?
10^6=2^x
6 ln10=x ln2
x=6 ln10/ln2=19.9 arrondi à 20.
il faut donc pousser un peu plus loin que la 12ème puissance.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
