Prouver qu'un ensemble est un ouvert
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par absolut-diabolik » 24 Nov 2011, 15:00
par absolut-diabolik » 24 Nov 2011, 15:00
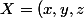 \in \mathbb{R}_{+}^3 ; x+y+z=1)
Je voudrais savoir comment prouver que cet ensemble un ouvert, avec la définition? ou complémentaire d'un fermé? je sais pas je suis perdue je ne sais pas du tout comment faire.
En fait, je m'explique j'ai une fonction
=x^ay^bz^c \quad\text{avec}\quad (a,b,c) \in \mathbb{R}_{+}^3.)
Il faut démontrer que cette fonction atteint son maximum sur X et calculer ce maximum.
Ou peut etre il faut démontrer que X est compact (dc fermé :mur:) et donc f atteint ses bornes sur X
Ou calculer les dérivées partielles, retrouver les points critiques et montrer que la matrice hessienne est définie négative (= ttes les valeurs propres sont négatives????) en ces points critiques . Mais dans ce cas
il faut que X soit ouvert.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 24 Nov 2011, 16:58
par Skullkid » 24 Nov 2011, 16:58
Bonjour, de ce que je comprends tu ne sais pas très bien si tu veux montrer que X est fermé et/ou ouvert et/ou compact... pour commencer ce serait bien d'avoir une idée de ce que tu veux montrer. Fais un dessin de X (dès qu'on te donne un ensemble dans R² ou R^3 qui a pas l'air trop moche, dessine-le, histoire de savoir de quoi tu parles), regarde-le dans le blanc des yeux, et essaye de voir s'il a plutôt une tête d'ouvert/de fermé/de compact.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
