Bonjour, je me présente je m'appel valentin et je suis au lycée. En math mon professeur nous à donner quelques exercices de révision sur les suites arithmétiques et je coince sur un petit exo.
Si vous pouvez m'exliquer la démarche à suivre sa serais génial.
Exercice: Soit [Un] une suite définie par Un=7-3n montrer que [Un] est une suite arthmétique et donner en la raison.
Je coince au niveau du montrer que [Un] est une suite arthmétique apres le reste je pense etre capable de le faire ^^ merci par avance pour toutes vos réponse.
Suite Arithmétique [Résolu]
13 messages
- Page 1 sur 1
omoikiru a écrit:(7-3n)²+1=r
D'où tu sors ça ?
Tu as
donc
D'où
Et pour l'écriture des formules, jette un coup d'oeil ici :
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
Attention aux indices !
 c'est U indice(n+1) c'est à dire le (n+1)ème terme de la suite.
c'est U indice(n+1) c'est à dire le (n+1)ème terme de la suite.
Une suite arithmétique :
Si tu donnes le premier terme de la suite, par exemple

et que la raison est 5
Ça veut dire que le deuxième terme de la suite sera

donc
Le troisième terme sera alors

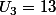
Donc en généralisant :

Et
*5)
(ou )
)
Tu remarques bien que
*5 -(3 + n*5))

 , 5 étant la raison.
, 5 étant la raison.
Donc adapte ça à ton exercice ...
Une suite arithmétique :
Si tu donnes le premier terme de la suite, par exemple
et que la raison est 5
Ça veut dire que le deuxième terme de la suite sera
donc
Le troisième terme sera alors
Donc en généralisant :
Et
(ou
Tu remarques bien que
Donc adapte ça à ton exercice ...
Ta suite est définie par :

Ce qui veut dire que le nième terme est égal à 7-3n
Donc le n+1ième terme est égal à 7-3(n+1)
donc
)
On a vu qu'en soustrayant le n+1ième et le nième, on obtient la raison (si on a une suite arithmétique)
Or ici
 - (7-3n) =-3)
avec des couleurs, si est en rouge et
est en rouge et  est en bleu
est en bleu
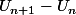 =7-3(n+1) - (7-3n)
=7-3(n+1) - (7-3n)
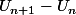 = -3 = la raison de ta suite
= -3 = la raison de ta suite
Tu as donc une suite arithmétique de raison -3 ...
Est ce que tu comprends ?
Ce qui veut dire que le nième terme est égal à 7-3n
Donc le n+1ième terme est égal à 7-3(n+1)
donc
On a vu qu'en soustrayant le n+1ième et le nième, on obtient la raison (si on a une suite arithmétique)
Or ici
avec des couleurs, si
Tu as donc une suite arithmétique de raison -3 ...
Est ce que tu comprends ?
Voilà. Et comme tu trouves -3, ça veut dire qu'on a bien une suite arithmétique, de raison -3
En effet, une suite arithmétique, c'est en fait une suite telle que à chaque fois que tu montes d'un rang, tu ajoutes un nombre, et ce nombre il est toujours le même (on va l'appeler r)
Donc entre le rang 6 et le rang 7, il y aura une différence de r, de même entre le rang 105 et le rang 106 etc ...
Mathématiquement parlant, le rang 6 se note , le rang 105 se note
, le rang 105 se note  etc ...
etc ...
Donc par exemple le rang 7, ce sera le rang 6 + ce nombre constant r
On a donc donc
donc 
Mais si jamais notre suite n'était pas arithmétique, nous n'aurions pas trouvé de r constant.
Comme on a trouvé -3 (et que -3 c'est constant, ça ne dépend pas de n) alors notre suite est arithmétique.
Il est très important de comprendre cette notion, elle reviendra plusieurs fois dans tout le lycée.
En effet, une suite arithmétique, c'est en fait une suite telle que à chaque fois que tu montes d'un rang, tu ajoutes un nombre, et ce nombre il est toujours le même (on va l'appeler r)
Donc entre le rang 6 et le rang 7, il y aura une différence de r, de même entre le rang 105 et le rang 106 etc ...
Mathématiquement parlant, le rang 6 se note
Donc par exemple le rang 7, ce sera le rang 6 + ce nombre constant r
On a donc
Mais si jamais notre suite n'était pas arithmétique, nous n'aurions pas trouvé de r constant.
Comme on a trouvé -3 (et que -3 c'est constant, ça ne dépend pas de n) alors notre suite est arithmétique.
Il est très important de comprendre cette notion, elle reviendra plusieurs fois dans tout le lycée.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
